[자동제어] 시스템의 수학적 모델과 블록 다이어그램
시스템의 수학적 모델
물리 시스템 속 다양한 미분 방정식
동작점에서의 선형 근사 모델
$y(t)-y_{0}=m(x(t)-x_{0}$
라플라스 변환
causal system 에서만 라플라스 변환
라플라스 변환에서 s는 differential operator로 생각할 수 있음
- s → $\Large{\frac{d}{dt}}$ 미분
- $\Large{\frac{1}{s} → \int^{t}_{0}dt}$ 적분
특성방정식
미분방정식을 변환하여 $Y(s) =p(s)/q(s)$ 로 나타냈을 때
denominator polynomial $q(s) = 0$ 이라하면, 이를 특성방정식이라 부름
- 이 방정식의 근이 시간 응답의 특성을 결정하기 때문
- 예를 들어 spring mass damper 시스템에서 $Y(s)=\frac{(s+3)y_{0}}{(s+1)(s+2)}$의 특성방정식은 (s+1)(s+2) 임
- 특성방정식의 근은 시스템의 poles라 부름
- numerator polynomial $p(s)=0$ 의 근은 zeros 라 부름
poles에서 Y(s)는 무한대가 되고, zeros에서 함수는 zero가 됨
최종치 정리 final value theorem
$y(t)$ 의 steady-state 값을 알고싶을때 사용할 수 있음
y(t)에서 t를 무한대로 보냈을 때 값은 lim s→0 일때 sY(s) 와 같음
- fvt 정리를 이용해 시스템의 steady-state 값을 쉽게 구할 수 있음
응용
전달함수가 G(s) 일때.. 입력에 따른 값을 구할 수 있음
Y(s) = G(s)U(s) 이고
sG(s)U(s) 를 0으로 보내면 됨.
위의 스프링 매스 댐퍼 시스템에서
입력이 impulse 응답이면 U(s)=1 이기에
최종치 정리fvt 에 의하면 답은 0
입력이 step 응답이면 U(s)=1/s 이기에
fvt에 의하면 답은 1.5
damping ratio 제타
특성방정식을 다음과 같이 나타낼 수 있음
$$s^{2}+2\zeta \omega_{n}s+\omega_{n}^{2}$$
이때 제타$\zeta$ 를 damping ratio라 하며 $\omega_{n}$을 natural frequency라 함
$\zeta$의 범위에 따라 특성방정식의 근의 형태가 아래 그림과 같이정해짐
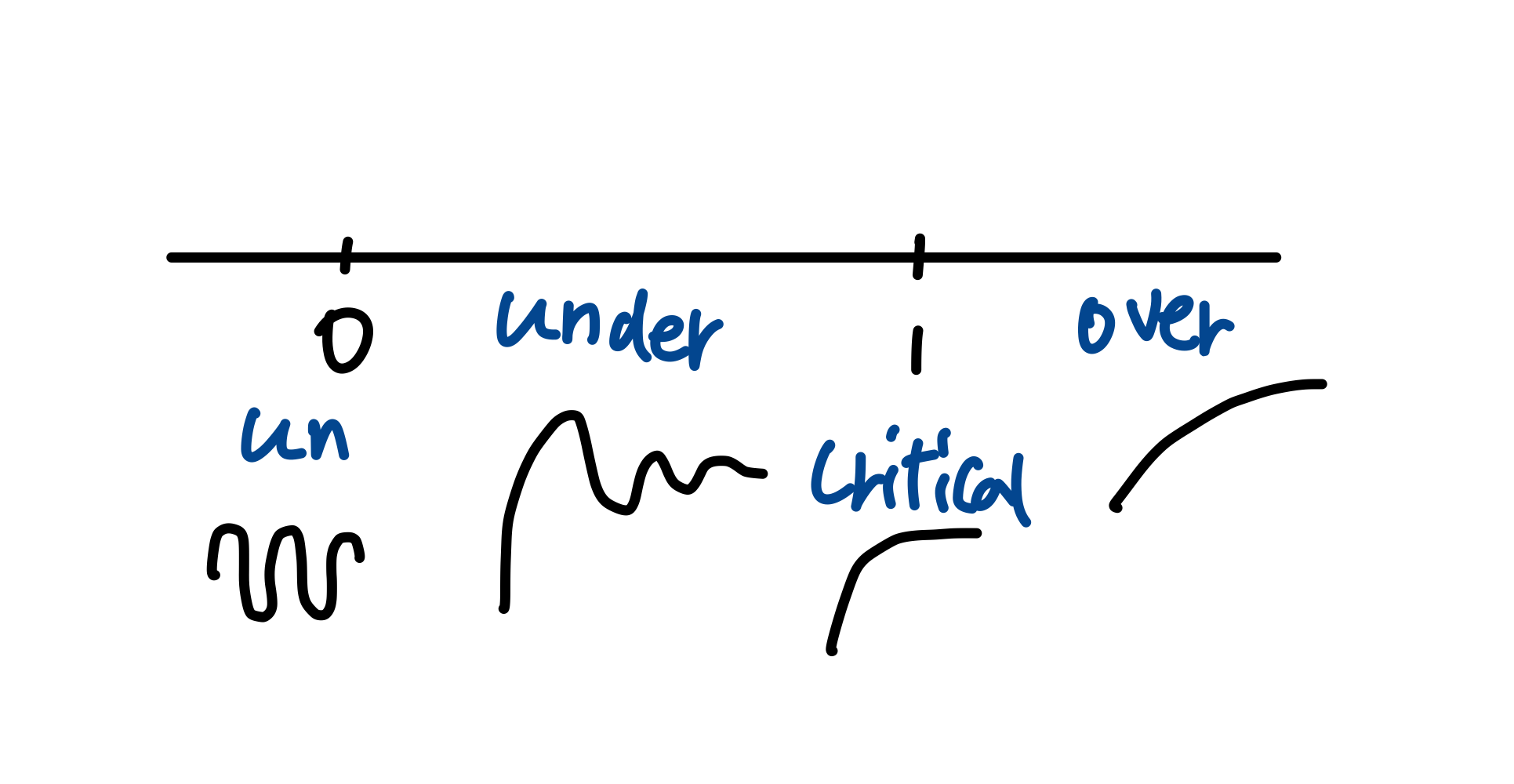
>1 overdamped (overdamping)
- 특성방정식 실근이 나옴
<1 underdamped (underdamping)
- 허근이 나옴
=1 critically damped (critical damping)
- (실수)중근이 나옴
=0 undamped (undamping)
- (허수)중근이 나옴
이처럼 steady 구간이 아닌 transient 구간에서 서로 다른 특징을 나타냄
라플라스 변환과 s-domain을 이용한 접근 방식은 transient 및 정상상태 응답을 위한 설계에 유용하다.
특성방정식의 해가 왼쪽 평면에서 더 멀어질수록 응답이 더 빠르게 감쇠할 것. 하지만 보통 시스템에서는 여러 개의 pole이 있고 transient 응답은 모든 poles 에 의한 응답이다.
Block Diagram Models
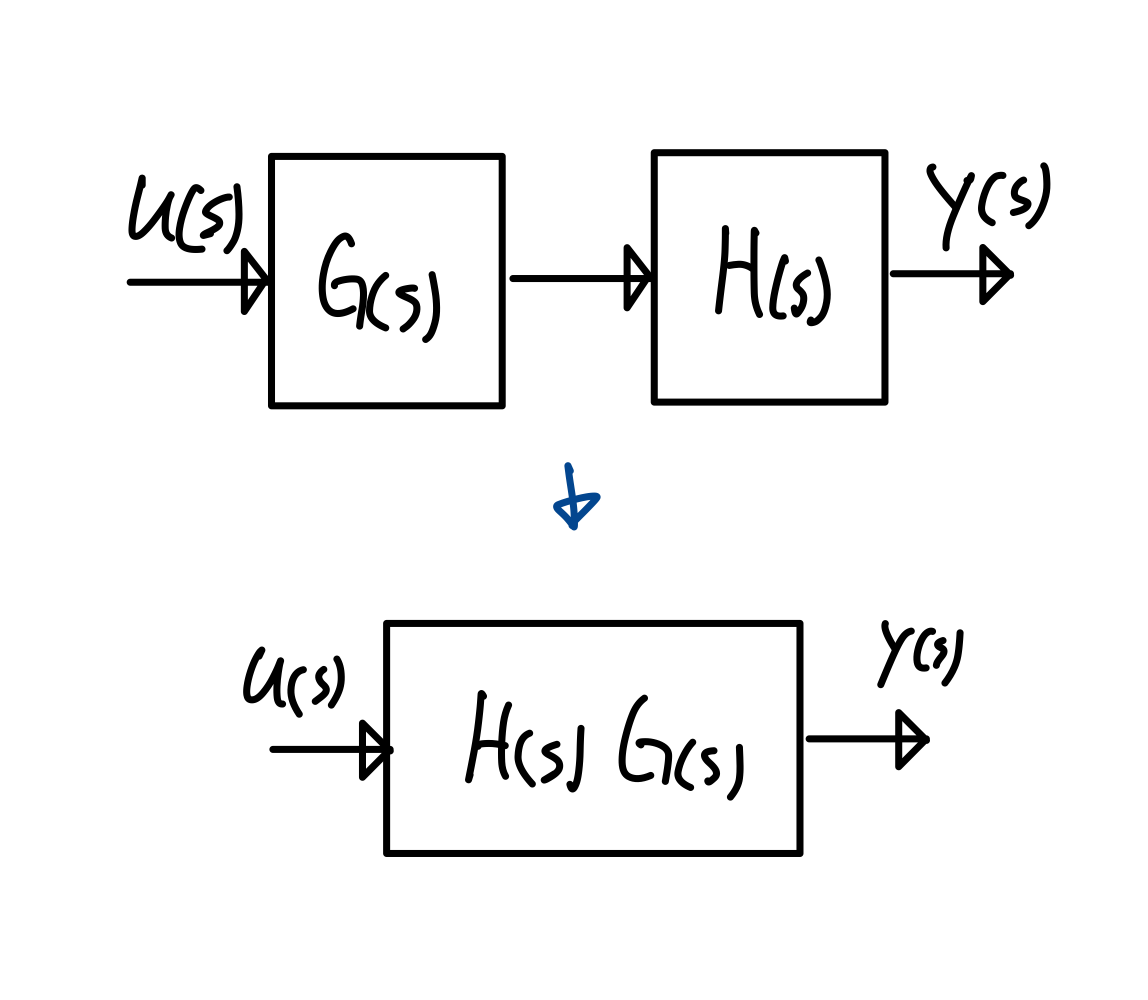
직렬 연결 → 곱 으로 나타나며 전달 함수의 합, 차 가능
블록 다이어그램에서 전달함수 구하기
- y에 대한 식, 타 변수에 대한 식을 구해 입출력으로만 구성되도록 연립해 풀이
전달함수 구하는 빠른 방법
closed-loop TF = forward path / (1+open-loop TF)
단 이때 폐루프의 전달함수는
피드백하는 함수가 빼지면(-) 1+open-loop TF
피드백 함수가 더해지면1-open-loop TF
block diagram reducing
꼬여있는 블록 다이어그램 reduce
피드백루프를 다른 피드백루프와 같은 지점에서 시작하도록 변형
- 전달함수를 변형해 지점을 미루거나 당기기
https://studentstory.tistory.com/330