티스토리 뷰
장면 속 물체의 움직임을 측정하는 것이 optical flow를 계산하는 문제이다.
먼저 3차원에서 점이 움직일 때 motion field 는 이미지에 대한 투영이다. 이미지에는 밝기 패턴만 있기에 Motion field를 측정할 수 없다. 영상에서 밝기 패턴의 움직임을 Optical Flow라 한다. Optical Flow Constraint Equeation으로 픽셀의 광학 흐름을 제한한다? 그리고 Optical flow를 추정하기 위한 Lucas-Kanade 방법을 알아보겠다.
영상 속 한 점이 3차원 장면에서 어떤 방향으로 움직이는 것을 생각해보자. 이 움직임은 이미지 평면에 투영되어 이미지 평면에서 움직임을 만들 것이다. 이를 움직이는 지점에 해당하는 `motion field` 라고 한다. 다만 이를 측정하는 것은 쉽지 않을 것이다.
🔷 Motion field
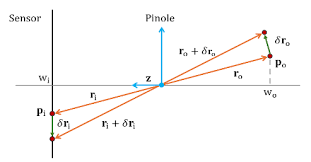
3차원에서 $\textbf{p}_{0}$ 인 점이 있고 이 위치는 $\mathbf{r}_{0}$ 벡터로 주어진다.
이 점에 대한 투영은 이미지에서 $\textbf{p}_{i}$ 로 나타나고 벡터는 $\mathbf{r}_{i}$ 이다.
점 $\textbf{p}_{0}$ 가 3차원 장면 속에서 어떤 속도 V₀를 가진다고 생각해보자. 이 점 $\textbf{p}_{0}$ 는 시간 $\Delta t$ 동안 이동하여 벡터 $\mathbf{r}_{0}+\Delta \mathbf{r}_{0}$ 로 주어지는 새로운 위치에 도달한다.
따라서 점의 속도 V₀는 벡터 $ \mathbf{r}_{0} $의 시간 변화율로, V₀ $= d \mathbf{r}_{0} / dt$ 이다. 우리가 관심을 갖는 것은 이 벡터가 이미지 평면으로 투영된 것이다.
그래서 이미지 평면에서 우리는 이미지 속도 $v_{i}$ 를 가지고 이는 $d\mathbf{r}_{i} / dt$ 시간변화율이다.
$$\mathbf{v}_{i}=f \frac{( \mathbf{r}_{0} \times \mathbf{v}_{0}) \times \mathbf{z}}{( \mathbf{r}_{0} \cdot \mathbf{z})^{2}}$$
🔷 Optical Flow
움직이는 카메라에 의해 촬영된 두 이미지가 있고 모션필드를 알고 싶다면 한 이미지의 밝기 패턴을 가져와서 두 번째 이미지에서 밝기 패턴이 어디로 이동했는지 확인할 수 있다. 확인할 수 있는 알고리즘이 있다면 각 펙셀이 어디로 이동하는지, 벡터를 얻을 수 있을 것이고 이 벡터가 해당 지점에서 Optical Flow 이다.
이상적으로는 optical flow가 motion field와 같을 것이다. 하지만 항상 그럴 수는 없다.
motion field와 optical flow를 찾을 수 없는 예시
- 모든 지점에서 동일한 반사율을 가진 구가 회전하고 있고, 광원이 있다면 모션필드는 존재하지만 optical flow는 없을 것이다.
- 마찬가지로 구가 있고 광원이 움직인다면 모션필드는 없지만 optical flow는 있을 것이다.
- 미용실 앞의 회전하는 원통형 간판을 생각하면 수평으로 회전하지만 이미지 패턴은 수직으로 움직인다.
Optical Flow 추정
제약 조건을 둬 개발한 optical flow constraint equation에 대해 알아볼 것이다.
먼저 짧은 간격으로 촬영된 두 이미지가 있다. $\delta t$ 동안 한 지점이 $(x,y)$에서 $(x+\delta x,y+\delta y)$로 이동 했다. 그렇다면 x와 y방향으로의 속도를 얻을 수 있다. $(u,v)=(\frac{\delta x}{\delta t}, \frac{\delta y}{\delta t})$
이 문제를 풀기위해 가정을 할 것이다.
Optical Flow의 기본 가정
- 밝기 보존 가정 (Brightness Constancy)
시간 $t$에 어떤 점의 밝기가 $I(x,y,t)$였다면, 이 점이 시간 $ t+ \delta t$ 후에 움직여서 $(x + \delta x, y + \delta y)$ 로 갔을 때도 밝기는 그대로라고 가정: $I(x,y,t)= I(x + \delta x, y + \delta y, t + \delta t)$ - 작은 이동 (Small Motion)
$\delta x, \delta y, \delta t$ 가 작다고 가정하고 1차 테일러 전개를 쓸 수 있음.
🔷 Optical Flow 방정식 유도
테일러 급수 전개
$$f(x+\delta x)=f(x)+\frac{\partial f}{\partial x} \delta x+ \cdots + \frac{\partial^{n} f}{\partial x^{n}} \frac{\delta x^{n}}{n!} $$
여기서 고차항들의 값이 매우 작아지기에 f(x)와 1차항만을 이용해 근사해 사용할 것이다.
밝기 보존 가정에 1차 테일러 전개를 적용하면
$I(x + \delta x, y + \delta y, t + \delta t) \approx I(x, y, t) + \frac{\partial I}{\partial x} \delta x + \frac{\partial I}{\partial y} \delta y + \frac{\partial I}{\partial t} \delta t$
Optical flow constraint eq
양변 빼면:
$0 \approx \frac{\partial I}{\partial x} \delta x + \frac{\partial I}{\partial y} \delta y + \frac{\partial I}{\partial t} \delta t$
양변을 $\delta t$로 나누면:
$\frac{\partial I}{\partial x} \frac{\delta x}{\delta t} + \frac{\partial I}{\partial y} \frac{\delta y}{\delta t} + \frac{\partial I}{\partial t} = 0$
여기서 시간에 대한 x의 미분값과 y의 미분값, 즉 속도를 얻을 수 있다.
때문에 다음과 같이 표기할 수 있으며 이것이 Optical Flow Constraint Equation 이다.
$I_{x} u + I_{y} v + I_{t} = 0$
- $u = \frac{\delta x}{\delta t}$ : x방향 속도 (flow)
- $v = \frac{\delta y}{\delta t}$: y방향 속도 (flow)
⚠️Aperture Problem
미지수가 두 개인데 방정식이 하나이다. 때문에 하나의 픽셀만으로는 flow를 구할 수 없다.
🔷 Lucas-Kanade 방법
앞서 본 것처럼 optical flow 추정 문제는 제약 조건이 부족하다.
지금부터 알아볼 Lucas_Kanade Method 는 매우 작은 영역에서의 optical flow가 해당 영역의 모든 점에 대해 동일하다는 가정을 사용한다.
방식
말한 것처럼 이미지에 작은 윈도우 W를 생각해보면 이 패치 내의 모든 점들이 동일한 optical flow를 생성한다.
그럼 이 윈도우 내의 각 점에 대해 $I_{x} u + I_{y} v + I_{t} = 0$ 를 만족할 것이다.
이 윈도우에는 많은 점이 있기에 점의 수만큼 방정식을 가진 큰 시스템을 얻게된다.
nxn 사이즈의 윈도우 W 의 모든 점들에 대해 같은 $u, v$ 를 가지면
$\forall (k,l) \in W, \quad I_{x}(k,l)u + I_{y}(k,l) v + I_{t}(k,l) = 0$
$A \begin{bmatrix} u \\ v \end{bmatrix} = \mathbf{b} $
- $A = \begin{bmatrix} I_{x}(1,1) & I_{y}(1,1) \\ I_{x}(k,l) & I_{y}(k,l) \\ \vdots & \vdots \\ I_{x}(n,n) & I_{y}(n,n) \end{bmatrix}, \quad \mathbf{b} = \begin{bmatrix} I_{t}(1,1) \\ I_{t}(k,l) \\ \vdots \\ I_{t}(n,n) \end{bmatrix} $
이 문제는 $n^{2}$ 방정식과 2개의 미지수를 푸는 최소제곱법으로 풀 수 있다.
최소제곱법
$Au=B$
$A^{T}A u=A^{T}B$
$\begin{bmatrix} u \\ v \end{bmatrix} = (A^T A)^{-1} A^T \mathbf{b}$
이것은 $A^{T}A$ 가 invertible 할때 가능하다.(즉 $\det (A^{T}A) \neq 0)
그리고 행렬이 well-conditioned, 즉 입력이 조금 바뀌어도 출력(밝기 변화)이 확실하게 바뀌어야 한다는 것이다.
- 좋은 상태의 조건과 예
- $ A^{T}A$ 행렬의 고유값이 둘 다 크고 비슷해야 한다. ($\lambda_{1} \approx \lambda_{2}$)
- 텍스쳐가 풍부한 영역: 질감이 많고 공간 기울기가 여러 방향으로 큰 영역 (고유값 비슷)
- 나쁜 상태의 예
- 예를 들어 벽과 같이 텍스쳐가 없고 단조로운 영역이면 고유값이 작다.
- 모서리: 한 방향으로만 기울기가 커 움직임을 정확히 알아내기 힘들다.(고유값 차이 큼)
'Computer Science > vision & ai' 카테고리의 다른 글
| 워드 임베딩(Word Embedding) 이란 (0) | 2025.06.03 |
|---|---|
| Attention 메커니즘과 Transformer 모델의 기본 구조 (0) | 2025.06.03 |
| NLP, RNN, LSTM, GRU 의 개념 (0) | 2025.06.02 |
| 베이즈 필터, 칼만 필터, 확장 칼만 필터 (0) | 2025.04.20 |
| 스테레오 비전 stereo vision 개념 및 활용 (0) | 2025.03.02 |
| [컴퓨터 비전] 카메라 모델과 파라미터의 이해 (0) | 2025.02.09 |
- Total
- Today
- Yesterday
- 교체
- Liiv M
- 메쉬 밴드
- 방향장
- 계산방법
- f-91w
- a모바일
- 문서 스캔
- 네이버페이
- mealy
- 알뜰 요금제
- 북문
- 카카오페이
- 배송기간
- 파스타
- 리브모바일
- 티스토리챌린지
- f-94w
- 알뜰폰요금제
- 10만포인트
- 오블완
- 알리익스프레스
- 밀리머신
- 맛집
- 카시오
- 무어머신
- 할인
- 리브엠
- 경북대
- 시계 줄
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
