[컴퓨터 비전] 카메라 모델과 파라미터의 이해

 

Euclidean coordinate vs Homogeneous coordinate

(평행이동 변환 예시)

유클리드 좌표 상 2차원의 한 point는 실수 쌍 (x, y)로 표현된다.
Homogeneous 좌표는 쉽게 말해 하나의 좌표를 추가해 (x,y,1) 와 같이 표현하는 것이다.

homogeneous 좌표에서 scale은 무시되기에
(x,y,1)과 (2x,2y,2)는 같은 point를 의미하며 더 나아가 (kx,ky,k) 또한 같은 point를 표현한다. 

때문에 역으로 유클리드 좌표를 구하기 위해서는 (x,y,w) 형태의 좌표를
끝 자리 수인 1로 나누어 (x/w,y/w,1) 형태로 만들고 유클리드 좌표인 (x/w,y/w)를 도출할 수 있다.

이처럼 2차원 공간에 대한 좌표를 투영(사영) 공간(projective space)?으로 확장시킬 수 있따.
유클리드 공간 $\mathbb{R}$의 point를 homogeneous vectors로 표현함으로써 투영 공간 $\mathbb{P}$으로 확장할 수 있다.

2차원 투영(사영) 공간의 무한대에 있는 point는 line을 형성함을 알 수 있다. (이는 line at infinity 로 불린다.)
3차원 공간에서는 평면을 형성할 것이다. 

 컴퓨터 비전에서 투영(사영) 공간은 실제 세계를 표현하는 방법으로 사용된다. 
이미지에서는 실제 세계를 2차원으로 투영함으로써 

평행이동 변환은 유클리드 좌표계에서 행렬로 표현하기 어렵지만 Homogeneous 좌표계에서는 행렬로 표현할 수 있다.
2차원의 한 point를 예시로 들면 유클리드 좌표에서는 (x,y), Homogeneous 좌표에서는 (x,y,1)이라 할 수 있다.
동차 좌표에서 평행이동을 행렬곱으로 표현할 수 있고 평행이동 행렬은 다음과 같다.

$T = \begin{bmatrix}
1 & 0 & t_{x} \\
0 & 1 &  t_{y}\\
 0& 0 & 1 \\
\end{bmatrix}$

---

Homogeneous coordinate에서의 직선의 방정식

일반적으로 직선의 방정식은 ax+by+c=0 으로 나타낼 수 있다.
homogeneous좌표에서 직선은 2차원 동차 좌표계에서 직선은 ax+by+cw=0 이며
좌표(x,y,w)가 만족해야하는 직선인 것이다.

혹은 $\mathbf{l}=[a,b,c]^{\top}$ 이고 $\mathbf{x}=[x,y,w]^{\top}$ 이라면 $l^{\top}\mathbf{x}=0$ 과 같이 직선을 표현할 수 있다.
$[a,b,c]^{\top}$로 표현할 수 있다. 
이와 같이 직선을 표현하면 아래처럼 두 직선의 교차점 등의 연산을 할 수 있다.

 

- 두 직선의 교차점

두 직선의 교차점은 다음과 같이 구할 수 있다.

$ l_{1}=(a_{1},b_{1},c_{1})$ 과 $l_{2}​=(a_{2}​,b_{2}​,c_{2}​) $에서

$p=l_{1}​\times l_{2}$

X 는 벡터의 외적을 의미하며 두 직선의 cross product를 구하면

$p = \begin{bmatrix} b_{1}c{2} - b_{2}c_{1} \\ a_{2}c_{1} - a_{1}c_{2} \\ a_{1}b_{2} - a_{2}b_{1} \end{bmatrix}​$

이유는 $l1^{\top}(l1\times l2)=0, l2^{\top}(l1\times l2)=0$

- 두 점을 지나는 직선

반대로 두 점을 지나는 직선은
두 점의 cross product로 구할 수 있다. 

$l=\mathbf{x}_{1} \times \mathbf{x}_{2}$

 

- 무한대 점

$w=0$인 점을 의미하며 즉 해당 point는 $p=(x,y,0)$ 으로 표현한다. 
유클리드 좌표계로 변환할 때 w로 나누는데 이 경우에는 무한대로 가기때문에
유클리드 좌표에서 무한대에 위치한다고 볼 수도 있다. 

예를 들어서 평행선의 교차점을 외적을 통해 구할 때
위와 같은 무한대의 점이 나오게 되는데 평행선은 무한히 먼 곳에서 교차한다고 해석할 수 있다.

---

핀홀 카메라 모델

핀홀 카메라 모델은 카메라의 이미지 형성과정을 단순화한 모델로
3차원 공간의 점을 이상적인 핀홀 카메라의 이미지 평면에 투영하는 수학적 관계를 설명한다.

이해를 위한 구성으로는

1. 핀홀: 빛이 통과하는 구멍으로 모든 빛이 해당 점(핀홀)을 지난다.
2. 이미지평면: 빛이 핀홀을 통과해 이미지가 형성되는 평면이다.
3. 초점거리(focal length): 핀홀과 이미지 평면 사이 거리이다.

가 있다.

핀홀카메라 모델은 이상적인 모델이기에 실제 세계에 적용하기에는 한계가 있다.

• 실제 카메라는 렌즈를 사용하지만 이 모델에는 렌즈가 없어 왜곡을 고려하지 않는다.
• 핀홀이 작으면 빛의 회절이 발생하지만 이를 무시한다.
• 초점 거리가 

 

- 카메라 투영 과정

- Euclidean coordinate

핀홀(centre of projection)을 유클리드 좌표계의 원점이라 생각해보자. 

보통 생각하는 핀홀 카메라는 핀홀을 지나 상이 거꾸로 맺히지만
image plane을 광선이 초점을 지나기 전에 위치시켰다.
때문에 아래 그림처럼 반전이 되지 않은 상으로 생각할 수 있다.

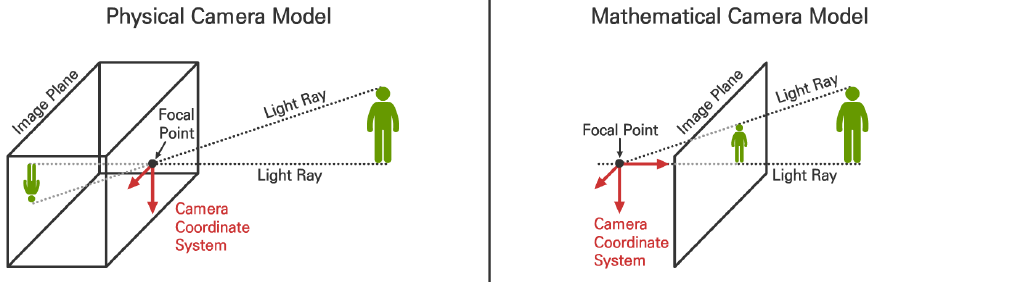
우리에게 익숙한 유클리드 좌표계로 생각한다면..
3차원 공간의 점(X,Y,Z)은 image plane의 $(f\frac{X}{Z},f\frac{Y}{Z})$ 가 된다.
이렇게 유클리드 3차원 공간 $\mathbb{R}^{3}$을 유클리드 2차원 공간 $\mathbb{R}^{2}$ 으로 매핑할 수 있었다. 

The centre of projection is called the camera centre. It is also known as the optical
centre. The line from the camera centre perpendicular to the image plane is called the
principal axis or principal ray of the camera, and the point where the principal axis
meets the image plane is called the principal point. The plane through the camera
centre parallel to the image plane is called the principal plane of the camera.

---

- Homogeneous coordinate

3차원에서 2차원으로 투영을 효과적으로 계산하기 위해서 homogeneous coordinate를 도입한다.
2차원은 z축이 추가되어 3차원 벡터 형태처럼 보이며, 3차원 벡터에도 한 차원을 추가한다. 

동차 좌표계 (Homogeneous Coordinates)를 사용하면
행렬곱을 통한 선형 매핑으로 매우 쉽게 표현할 수 있다.

가장 기초적인 핀홀 카메라 모델은 다음과 같은 행렬곱으로 쓸 수 있다.
3차원에 2차원으로의 투영을 다음과 같이 표현할 수 있다.
$\mathbf{x} = \texttt{P}\mathbf{X}$
이를 $x=f \cdot \frac{X}{Z}, y=f \cdot \frac{Y}{Z} $ 가 나오도록 아래처럼 쓸 수 있고

$ \begin{pmatrix} X\\Y\\Z\\1 \end{pmatrix} \mapsto \begin{pmatrix} fX\\fY\\Z \end{pmatrix} = \begin{bmatrix} f&&&0 \\ &f&&0\\&&1&0 \end{bmatrix} \begin{pmatrix} X\\Y\\Z\\1 \end{pmatrix}$

$\mathbf{x} = \texttt{P}\mathbf{X}$에서 $\texttt{P}$ 를 camera projection matrix 라 한다. ($\texttt{P} = diag(f,f,1)[I | 0]$)

---

p 점이 축에 있지 않다면?   

• 처음 핀홀카메라를 설명할 때 이미지 평면의 원점과 카메라 핀홀(원점)이 같은 축에 있다고 가정했다.
  하지만 아래 사진처럼 p 점이 $p_{x}, p_{y}$ 에 위치한다면?
  
  즉 카메라 좌표계와 이미지평면의 좌표계가 다르다.

• $\begin{pmatrix} X\\Y\\Z\\1 \end{pmatrix} \mapsto  \begin{pmatrix} fX+Zp_{x}\\fY+Zp_{y}\\Z \end{pmatrix} = \begin{bmatrix} f&&p_{x}&0 \\ &f&p_{y}&0\\&&1&0 \end{bmatrix} \begin{pmatrix} X\\Y\\Z\\1 \end{pmatrix}$

---

camera matrix의 일반화

또한 실세계(World) 좌표와 카메라 좌표가 다르기 때문에 변환이 필요하다.

• 기존의 $\mathbf{x} = \texttt{P}\mathbf{X}$ 에서 $ \mathbf{X} $ 이 아닌 $ \mathbf{X}_{cam}$ 으로 볼 수 있다.
• 즉 우측 World 좌표에서의 좌표를 회전과 이동 변환으로 카메라 좌표축으로 변환하고 
  투영 matrix가 필요하다.
  • $\mathbf{X}_{cam} = \begin{bmatrix} \texttt{R} & -\texttt{R} \tilde{\texttt{C}} \\
    0 & 1 \\ \end{bmatrix} \begin{pmatrix} X\\Y\\Z\\1 \end{pmatrix} =  \begin{bmatrix}
    \texttt{R} &- \texttt{R} \tilde{\texttt{C}} \\ 0 & 1 \\ \end{bmatrix} \mathbf{X}$ 으로 나타낼 수 있으
• 즉 ①카메라, ②이미지, ③월드 좌표계가 다른 것을 전부 고려하면 다음과 같은 식을 도출해낼 수 있다.
  
  $x =\texttt{K}[I|0]\mathbf{X}_{cam} = \begin{bmatrix} f&0&p_{x} \\ 0&f&p_{y}\\0&0&1 \end{bmatrix} [I | 0] \mathbf{X}_{cam} 
  =  \begin{bmatrix} f&0&p_{x} \\ 0&f&p_{y}\\0&0&1 \end{bmatrix} [I | 0] \begin{bmatrix}
  \texttt{R} & - \texttt{R} \tilde{\texttt{C}} \\ 0 & 1 \\ \end{bmatrix} \mathbf{X} $ 
• 다시 보면 matrix$\texttt{K}= \begin{bmatrix} f&0&p_{x} \\ 0&f&p_{y}\\0&0&1 \end{bmatrix} $ 이 image to image Transformation을 수행하며 내부 파라미터(intrinsic parameter)라 한다.

---

외부 파라미터 extrinsic parameter

내부파라미터 뒤에 있는 행렬은 다음과 같이 쓸 수도 있다.

$x= \begin{bmatrix} f&0&p_{x} \\ 0&f&p_{y}\\0&0&1 \end{bmatrix} [I | 0] \begin{bmatrix}
\texttt{R} & - \texttt{R} \tilde{\texttt{C}} \\ 0 & 1 \\ \end{bmatrix} \mathbf{X} = \begin{bmatrix} f&0&p_{x} \\ 0&f&p_{y}\\0&0&1 \end{bmatrix} \begin{bmatrix}
\texttt{R} & - \texttt{R} \texttt{C}  \\ \end{bmatrix} $

 $ \begin{bmatrix} \texttt{R} & - \texttt{R} \texttt{C}  \end{bmatrix} $ 행렬은 World to Camera Transformation을 수행하며 외부 파라미터(extrinsic parameter)라 한다.

카메라 파라미터 K[R|-RC] 는 $\texttt{K}[\texttt{R}|\texttt{t}]$ 로 쓸 수도 있고
여기서 외부 파라미터 행렬(3 x 4)는 $\texttt{R}$과 $\texttt{t}$ 로 볼 수 있는데 R은 3D rotation, t는 3D translation을 의미한다.
$[R|t] =\begin{bmatrix} r_{1} & r_{2} & r_{3} & t_{1} \\ r_{4}& r_{5} & r_{6} & t_{2} \\ r_{7}&  r_{8}& r_{9} & t_{3} \\ \end{bmatrix} $ 

---

Calibration (DLT, Zhang’s method)

카메라의 파라미터를 구하는 과정을 Geometry Calibration이라 한다.

 

예를 들어 점들의 집합 $\mathbf{x}_{i}$와 $\mathbf{x}_{i}'$의 대응에서 2차원 사영변환을 추정할 수 있다. 
각 $i $에 대해 $H \mathbf{x}_{i}=\mathbf{x}_{i}'$가 되도록 3 x 3 행렬 H를 계산하는 것이다. 

필요한 변수의 수

matrix H를 구하기 위해 필요한 대응점 $ \mathbf{x}_{i} \leftrightarrow \mathbf{x}_{i}' $쌍의 개수를 생각해야 한다. 

DoF(Degrees of Freedom) 자유도라고 부르며 Transform 시 필요한 독립변수의 수 
translation 의 DoF는 2
이동 후 회전 3
이동,회전,축소 4
affine 6
projective 8

2차원 변환은 8의 자유도를 가진다. 첫 번째 점은 두번 째 이미지에서 자유도 2를 가진다? 때문에 H를 결정하려면 4개의 점 대응이 필요하다

---

- Direct Linear Transformation (DLT)

각 대응점 ($X_{i}, Y _{i}, Z _{i}) \leftrightarrow (x_{i}, y_{i})$은 다음 두 방정식을 생성한다.

카메라 투영 행렬 3 x 4 크기로 $\texttt{P}=\begin{bmatrix} p_{11}&p_{12}&p_{13}&p_{14} \\ p_{21}&p_{22}&p_{23}&p_{24} \\ p_{31}&p_{32}&p_{33}&p_{34} \end{bmatrix}$ 이기에 

$x_{i} =\frac{p_{11}X_{i}+p_{12}Y_{i}+p_{13}Z_{i}+p_{14}}{p_{31}X_{i}+p_{32}Y_{i}+p_{33}Z_{i}+p_{34}}, y_{i} =\frac{p_{21}X_{i}+p_{22}Y_{i}+p_{33}Z_{i}+p_{24}}{p_{31}X_{i}+p_{32}Y_{i}+p_{33}Z_{i}+p_{34}}$  

$x_{i}(p_{31}X_{i}+p_{32}Y_{i}+p_{33}Z_{i}+p_{34}) =p_{11}X_{i}+p_{12}Y_{i}+p_{13}Z_{i}+p_{14}$
$y_{i} (p_{31}X_{i}+p_{32}Y_{i}+p_{33}Z_{i}+p_{34})=p_{21}X_{i}+p_{22}Y_{i}+p_{33}Z_{i}+p_{24}$

여기서 i~n 까지 모든 대응점을 넣고 결합하면
$A = \begin{bmatrix}
X_{1} & Y_{1} & Z_{1} & 1 &0 & 0 & 0 & 0& -x_{1}X_{1}&-x_{1}Y_{1}&-x_{1}Z_{1}&-x_{1} \\
0 & 0 & 0 & 0 & X_{1} & Y_{1} & Z_{1} & 1 & -y_{1}X_{1}&-y_{1}Y_{1}&-y_{1}Z_{1}&-y_{1} \\
\vdots & \vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots   \\
X_{n} & Y_{n} & Z_{n} & 1 & 0 & 0 & 0 & 0  & -x_{n}X_{n}&-x_{n}Y_{n}&-x_{n}Z_{n}&-x_{n} \\
0 & 0 & 0 & 0 & X_{n} & Y_{n} & Z_{n} & 1  & -y_{n}X_{n}&-y_{n}Y_{n}&-y_{n}Z_{n}&-y_{n} \\
\end{bmatrix}, \mathbf{p} =\begin{bmatrix}
 p_{11}\\p_{12}\\p_{13}\\p_{14}\\p_{21}\\p_{22}\\p_{23}\\p_{24}\\p_{31}\\p_{32}\\p_{33}\\p_{34}\\
\end{bmatrix}$

$A \mathbf{p} = 0$ 임을 이용하여 
행렬 A에 SVD를 적용하여 $A=U\sum V^{T}$

V의 마지막 열이 최소 특이값에 대응하는 해 $\mathbf{p}$ 이다. 
$\mathbf{p}$ 를 행렬 $\mathbf{P}$로 재구성한다. 

SVD(Singular Value Decomposition)
특이값 분해 방법?
m x n 행렬 A가 있을 
$A=U\sum V^{T}$ 에서 U (m x m)와 V (n x n)는 직교행렬이고 $\sum$ (m x n)대각행렬이다.
때문에 Ax는 x를 $V^{T}$에 의해 회전시키고, $\sum$로 스케일을 조정한 다음, 다시 U로 회전시키는 것이다.

$A^{T}A$ 의 고유벡터가 V의 열벡터
$AA^{T}$ 의 고유벡터가 U의 열벡터
고유값의 제곱근이 $\sum$의 특이값이다. 

V의 마지막 열이 $\sum$ 에서 0에 가장 가까운 특이값에 대응한다.

구한 행렬 $\mathbf{P}$에서 K와 R과 C를 구해야한다.
$P=K[R|-RC]$ 이기에 =[H|h] 로 생각해보자(H=KR 이고 h=-KRC)
그러면 $H^{-1} =(KR)^{-1}=R^{-1}K^{-1}=R^{\top}K^{-1}$

이전에 설명했다시피 R은 rotation matrix이고 
QR 분해로 $\mathbf{P}$를 $R^{\top}, K^{-1}$로 분해할 수 있다. 

- QR분해란?

[선형대수] Gram-Schmidt process와 QR 분해

 

2차원에서 2차원으로의 대응에서 $\texttt{H}$ 를 결정하기 위한 가장 간단한 선형 알고리즘이다.
변환은 $ \mathbf{x}_{i}' = \texttt{H}\mathbf{x}_{i}$ 라 할 수 있다. 
(같은 벡터가 아닌 방향이 같은 것이다)

matrix H 를 다음과 같이 표기할 수도 있다.

$ \texttt{H} = \begin{bmatrix}
h_{1} &h_{2}  &  h_{3}\\
 h_{4}&  h_{5}& h_{6} \\
h_{7} &h_{8}  &  h_{9}\\
\end{bmatrix} = \begin{bmatrix} h^{1 \top} \\ h^{2 \top} \\ h^{3 \top} \end{bmatrix}$ 이고 $ \texttt{H} \mathbf{x}_{i} = \begin{pmatrix} h^{1 \top}\mathbf{x}_{i} \\ h^{2 \top}\mathbf{x}_{i} \\ h^{3 \top}\mathbf{x}_{i} \end{pmatrix}$

이때 조금 헷갈리는데 $\mathbf{h}^{1 \top}$가 $\texttt{H}$의 1번째 행이다.
때문에 $\mathbf{h}^{1}$은 $\begin{pmatrix}
h_{1}\\
h_{2} \\ h_{3}
\end{pmatrix}$ 을 의미한다.

1. 방정식 설정

$\mathbf{x}_{i}'= (x_{i}', y_{i}', z_{i}')^{\top}$로 표기하면 벡터 외적을 다음과 같이 표기할 수 있다.  

$\mathbf{x}_{i}' \times \texttt{H} \mathbf{x}_{i} = \begin{pmatrix}
y_{i}'h^{3\top}\mathbf{x}_{i} - \omega_{i}'h^{2\top}\mathbf{x}_{i} \\
\omega_{i}'h^{1\top}\mathbf{x}_{i} - x_{i}'h^{3\top}\mathbf{x}_{i} \\ x_{i}'h^{2\top}\mathbf{x}_{i} - y_{i}'h^{1\top}\mathbf{x}_{i}
\end{pmatrix} $

~ 이므로 ??? 다음과 같은 세 개의 방정식을 얻을 수 있다.

$\begin{bmatrix}
0^{\top} & -\omega_{i}'\mathbf{x}_{i}^{\top} & y_{i}'\mathbf{x}_{i}^{\top} \\
\omega_{i}'\mathbf{x}_{i}^{\top} & 0^{\top} & -x_{i}'\mathbf{x}_{i}^{\top} \\
-y_{i}'\mathbf{x}_{i}^{\top} &  x_{i}'\mathbf{x}_{i}^{\top}&  0^{\top}\\
\end{bmatrix}  \begin{pmatrix}
\mathbf{h}^{1} \\
\mathbf{h}^{2} \\ \mathbf{h}^{3}
\end{pmatrix}=0$

앞의 행렬은 3 x 9 행렬이고 $\mathbf{h}$는 9x1 벡터이다?

방정식이 세 개지만 두 개만 선형 독립이기에 H 원소에 대한 방정식 두 개를 얻을 수 있다. 이후 방정식은 다음과 같다.
이 행렬은 2 x 9 크기를 가지며 matrix $A_{i}$라 하겠다. 

$\begin{bmatrix}
0^{\top} & -\omega_{i}'\mathbf{x}_{i}^{\top} & y_{i}'\mathbf{x}_{i}^{\top} \\
\omega_{i}'\mathbf{x}_{i}^{\top} & 0^{\top} & -x_{i}'\mathbf{x}_{i}^{\top} \\
\end{bmatrix}  \begin{pmatrix}
h^{1} \\
h^{2} \\h^{3}
\end{pmatrix}=0$

2. 해법
점 대응쌍 네 개에서 연립방정식을 풀어야하며 trivial sol. 인 $\mathbf{h}=0$에 관심이 없기에 0이 아닌 해를 찾아야 한다.

1. 위 처럼 행렬 $A_{i}$ 를 만든다.
2. 대응되는 쌍이 n개라면 n개의 2 x 9 행렬 $A_{i}$를 모아 하나의 2n x 9 행렬 A를 만든다.
3. A의 SVD를 구한다. 가장 작은 특이값에 해당하는 단위 특이 벡터가 해 $ \mathbf{h}$가 된다.
   ($\texttt{A}=UDV^{T}$이며 $\mathbf{h}$ 는 마지막 행이다???
4. $\mathbf{h}$ 에서 $\texttt{H}$ 행렬로 재구성한다.

 

 

---

- Zhang’s method

앞서 DLT에서는 내부 파라미터와 외부 파라미터 모두 구할 수 있었다. 
이번에 알아볼 Zhang's method에서는 5개의 파라미터만 구할 수 있다.

이 방법에서는 체커보드를 이용해 캘리브레이션을 진행하는데 체커보드 평면을 z=0인 평면이라 가정한다. 
때문에 체커보드 위의 모든 point의 z좌표가 0이며 외부파라미터 matrix의 3번째 열을 삭제할 수 있다. 

$x=  \begin{bmatrix} f&0&p_{x} \\ 0&f&p_{y}\\0&0&1 \end{bmatrix} \begin{bmatrix} r_{1} & r_{2} & r_{3} & t_{1} \\ r_{4}& r_{5} & r_{6} & t_{2} \\ r_{7}&  r_{8}& r_{9} & t_{3} \\ \end{bmatrix}  \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix} \to   \begin{bmatrix} f&0&p_{x} \\ 0&f&p_{y}\\0&0&1 \end{bmatrix} \begin{bmatrix} r_{1} & r_{2}  & t_{1} \\ r_{4}& r_{5}  & t_{2} \\ r_{7}&  r_{8} & t_{3} \\ \end{bmatrix} \begin{bmatrix} X \\ Y \\ 1 \end{bmatrix} $

이 식을 해결하기위해 DLT와 같은 과정으로 matrix를 추정한다.
각 point 당 2개의 선형방정식이 만들어지기에 파라미터를 추정하기 위해서는 
최소 4개의 point가 필요하다. 

DLT 방법처럼 파라미터를 구하고 마찬가지로 분해를 해야 3 x 3 행렬 K를 알아낼 수 있다.
방법은 우선 H=K[r1, r2, t] 형태에 K^{-1} 을 곱한다.
$ [r_{1}, r_{2}, t]=K^{-1}H = K^{-1}[h_{1}, h_{2}, h_{3}] $

$\to r1=K^{-1}h_{1}, r2=K^{-1}h_{2}$

r1 r2는 orthonormal basis 이므로 아래 식을 만들 수 있다.
$r_{1}^{\top}r_{2}=0$ 이므로 $ h_{1}^{T}K^{-\top}K^{-1}h_{2}=0$

r1과 r2의 크기가 1이므로 $ h_{1}^{T} K^{-T}K^{-1}h_{1}-h2^{T}K^{-T}K^{-1}h_{2}=0$

이 식들에서 $K^{-T}K^{-1}$ 을 matrix B 라고 정의하면
$h_{1}^{T}Bh_{2}=0$
$ h_{1}^{T}Bh_{1} - h_{2}^{T}Bh_{2} =0$

$AA^{T}$와 같은 형태는 Cholesky decomposition 으로 분해할 수 있는데 이 방법을 쓰기 위해서는 우선 B부터 구해야한다. 
Vb=0 을 구성하고 이를 구하기 위해 여러 이미지가 필요하다.
여러 이미지로 해당 식을 구성하고 Trivial sol을 갖지 않도록 b의 크기가 1이라는 조건을 추가한다.
현실에서 측정에서 노이즈를 최소화하기 위해 square 에러를 최소화 하는 해를 찾아야한다.
이는 다음과 같다.

b*= arg min ||Vb|| with ||b||=1

DLT와 같이 풀고 B를 얻은 후 내부 파라미터를 구할 수 있다.