티스토리 뷰
Orthogonal vector
orthogonal 이란 직교를 의미한다.
orthogonal set의 p개 벡터는 서로 orthogonal 하다. 서로 수직이기에 내적은 0이 될 것이다.
orthogonal set이 0벡터가 없는 집합이라면 이 집합은 선형 독립이며 동시에 S에 span되는 subspace의 basis이다.
Orthogonal basis는 basis이면서 동시에 orthogonal한 경우를 말한다.
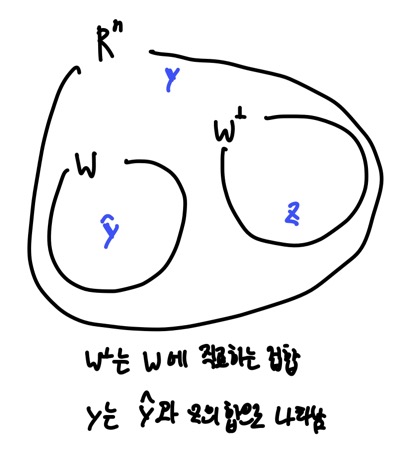
Orthogonal Decomposition
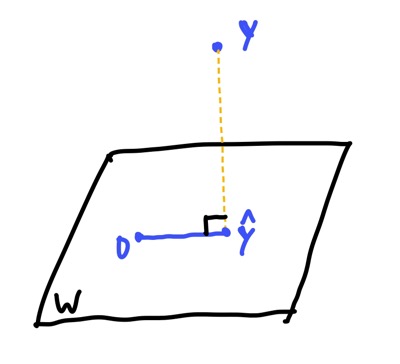
$y = \hat{y}+z $ $\hat{y}$ 은 W에서 y에 가장 가까운 W위의 유일한 벡터
y에서 W에 수선의 발을 내린것과 마찬가지
Gram-Schmidt process
Gram Schmidt 과정은 선형독립인 k개의 벡터에서 k개의 직교 벡터를 생성하는 방법이다.
$\mathbf{R}^{n}$ 의 nonzero subspace 의 basis ${\mathbf{x}_{1}, \mathbf{x}_{2}}$ 로 orthonormal basis $ {\mathbf{v}_{1}, \mathbf{v}_{2}} $찾기
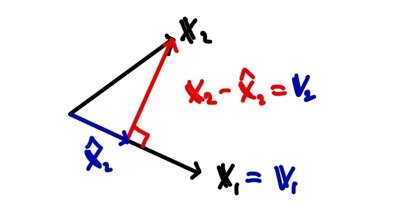
방법은 다음과 같다.
- 행렬 A의 열 벡터 중 하나인 $\mathbf{x}$ 를 $\mathbf{v}$ 으로 삼는다.
- $\mathbf{x}_{2}$ 에서 $\mathbf{x}_{1}$ 에 수선의 발을 내려 수직인 벡터를 찾는다.
- $\hat{\mathbf{x}_{2}}= \Large{\frac{ \mathbf{x}_{2}\cdot \mathbf{x}_{1}}{ \mathbf{x}_{1}\cdot \mathbf{x}_{1}}}$
- 수직인 벡터 : $\mathbf{v}_{2}= \mathbf{x}_{2} - \hat{\mathbf{x}_{2}} $
이렇게 구한 Orthogonal basis를 크기가 1인 벡터로 정규화를 거치면 Orthonormal(정규 직교) basis가 된다.
QR Factorization
QR 분해는 (m x n) matrix $A=[\mathbf{x}_{1} \cdots \mathbf{x}_{n}]$ 에서 A의 직교 열벡터로 구성된 행렬 Q와 상삼각행렬 R의 곱으로 분해하는 과정으로, $A=QR$로 나타낼 수 있다.
(m x n 행렬 A의 벡터가 선형 독립일 때)
Q는 Gram-schmidt 방법으로 구한 (m x n) 크기의 Orthonormal basis의 집합이며
R은 (n x n) 크기의 Upper triangle matrix이다.
QR분해 과정
- Q 구하기
- Gram-Schmidt 방법으로 A의 Orthonormal basis를 구한다.
- R 구하기
- 구한 Q의 column이 orthonormal하므로 $Q^{\top}Q=I$ 가 성립한다.
- 때문에 $Q^{\top}A=R$ 이 성립하므로 R을 구할 수 있다.
QR분해를 이용한 최소제곱법
먼저 QR분해가 가능한 행렬 A에 대해 Gram Schmidt 방법으로 $A=QR$로 분해해준다.
$A \mathbf{x} =b$ 에서 $||A \mathbf{x}-b||$ 가 최소가 되는 $\mathbf{x}$를 구해야 한다.
$A\mathbf{x}$ 가 column space Col A에 속하는데 최소제곱해는 해당 공간에서 b에 가장 가까운 점을 의미한다.
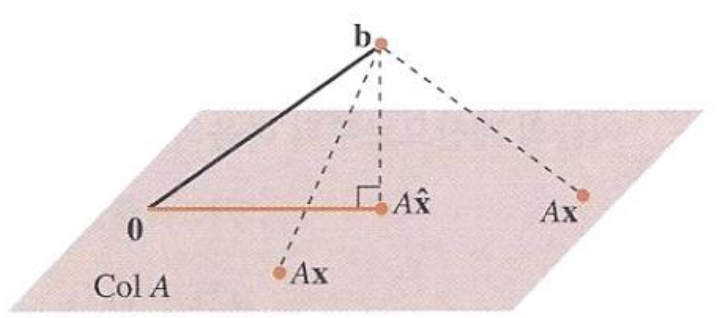
이를 만족하는 해를 $\hat{\mathbf{x}}$ 라 하면
QR 분해를 이용해 얻을 수 있는 최소 제곱해는 다음과 같다
$\hat{\mathbf{x}}=R^{-1}Q^{T}b$
그 이유는 먼저 $QR \hat{\mathbf{x}} = b$ 로 쓸 수 있고
$(R^{T}Q^{T}) QR hat{\mathbf{x}} = R^{T}Q^{T}b$
이는 $R^{T}R \hat{\mathbf{x}}=R^{T}Q^{T}b$ 와 같고 아래와 같이 바뀐다.
$R \hat{\mathbf{x}}=Q^{T}b$
다시 Ax=b에 대입해도 아래와 같이동일한 결과가 나옴을 알 수 있다.
$A \hat{\mathbf{x}} = QR \hat{\mathbf{x}}=QRR^{-1}Q^{T}b = QIQ^{T}b = QQ^{T}b$
'전기전자공학 > 수학' 카테고리의 다른 글
| 행렬식과 Eigenvalue & Eigenvector (0) | 2025.03.05 |
|---|---|
| [선형대수] Linear Transformation (0) | 2025.02.11 |
| 인공지능을 위한 선형대수 & 확률과 통계 (0) | 2025.02.04 |
| [수학] 자연성장, 감소/로지스틱 방정식 (1) | 2020.05.31 |
| [수학] 미분방정식, 방향장, 오일러 방법 (0) | 2020.05.31 |
| [수학] 리만합과 근삿값 (0) | 2020.05.31 |
| [수학] 특이적분 (0) | 2020.05.31 |
| [수학] 삼각함수와 적분 (0) | 2020.05.31 |
- Total
- Today
- Yesterday
- 문서 스캔
- f-91w
- 리브모바일
- 티스토리챌린지
- 방향장
- 밀리머신
- 알뜰폰요금제
- 알리익스프레스
- 카카오페이
- 카시오
- 알뜰 요금제
- 시계 줄
- 메쉬 밴드
- 10만포인트
- 교체
- 파스타
- 북문
- 무어머신
- f-94w
- 경북대
- 배송기간
- 오블완
- a모바일
- 네이버페이
- 계산방법
- 할인
- mealy
- Liiv M
- 맛집
- 리브엠
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |

