[선형대수] Linear Transformation

Linear Transformation

Linear Transformation 은 Linear Mapping, Linear Map 선형변환, 선형사상, 선형함수 등으로도 불린다.

선형변환은 행렬로 표현될 수 있는데, 예를 들어 n차원 벡터 $\mathbf{x}$ (m x n) 행렬 A를 곱하면 m차원 벡터가 얻어진다. 행렬A로 인해 다른 벡터로 옮기는 변환이 결정된 것이다. 단순한 하나의 예시로는 점을 점으로 옮기는 이미지가 연상되지만 공간이 행렬로 인해 어떻게 변하는지 떠올려야한다. 

$A=\begin{pmatrix} 1&-0.3\\0.7&0.6 \end{pmatrix}$ 와 같은 행렬에 의해 공간이 어떻게 변하는지 떠올리기 위해서는
다음과 같이 생각할 수 있다.

$e_{1} = \begin{pmatrix} 1\\0 \end{pmatrix} e_{2}= \begin{pmatrix} 0\\1 \end{pmatrix} $ 을 각각 $\begin{pmatrix} 1\\-0.7 \end{pmatrix}$와  $\begin{pmatrix} -0.3\\0.6 \end{pmatrix}$ 로 이동시킨다. 

행렬의 곱도 이처럼 이해할 수 있다. $\mathbf{z}=BA\mathbf{x}$ 에서 $\mathbf{x}$를 A를 이용해 $\mathbf{y}$로 변환한다. $\mathbf{y}$를 B를 이용해 $\mathbf{z}$로 변환한다. 
이 과정을 행렬곱 BA를 이용해 한번에 z로 변환하는 것이다. 

 

Ax=b 에 대한 해석도 두 가지로 볼 수 있다.

1. A column들에 대한 linear combination으로 b가 만들어진다.
2. A에 의해 x가 b로 transform 된다. 

2번의 관점에서 보면 행렬 A(m x n)에 의한 transform은 $T : \mathbb{R}^{n} \to \mathbb{R}^{m}$

아래 그림에서 transformation T에 의한 x의 이미지는 T(x)이다.

T는 행렬 A에 의해 정의역(Domain)에서 공역(Codomain) 으로 매핑이 되며 
만약 모두 독립이라면 공역은 치역(Range)과 같다.

예를 들어 3 x 3 행렬에서 모두 독립이라면 $\mathbb{R}^{3}$를 span하며 공역=치역 이다.
다만 2개만 독립이라면 평면이라고 볼 수 있기에 치역은 공역의 일부라 볼 수 있다. 

 

위의 transformation에서 Linear Transformation이 되기 위한 조건은 다음과 같다. 

1. f(u+v)=f(u)+f(v)
2. f(cu)=cf(u)

이 조건을 확장하면 T가 선형이면 $T(c_{1}v_{1}+\cdots +c_{p}v_{p})=c_{1}T(v_{1})+ \cdots +c_{p}T(v_{p})$

때문에 T(x)=$\mathbf{Ax}$로 표현되는 것은 모두 Linear Transform이다. 

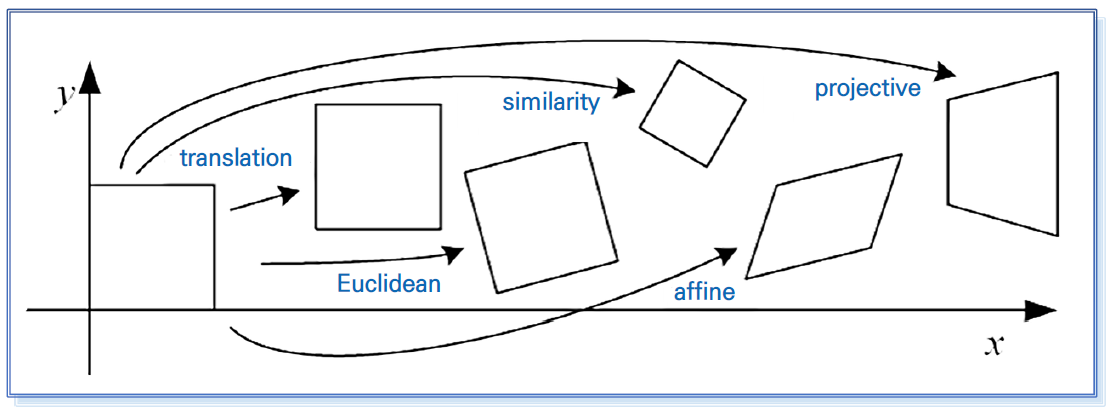
2D Transformation

위치를 평면이동하는 translation
translation에 회전까지 고려한 Euclidean
scale까지 고려한 similarity
변형이되었지만 평행이 유지가 된 affine 변환
투영과 관련된 projective 변환 이 있다.

1. Translation 

크기, 각도, 면적을 유지하며 위치만 이동하는 경우이다. 
x' = x + t_{x}
y' = y+t_{y}

다만 translation을 2x2 행렬 M으로 표현하기에는 문제가 따르며 
이를 해결하기 위해서는 homogeneous 좌표계가 필요하다. 

알다시피 성분 1을 추가하여 3차원 형태로 나타내며 
결국 translation 변환 행렬은 다음과 같이 정의할 수 있다.

$\begin{bmatrix}
x'\\
 y'\\1
\end{bmatrix}=
\begin{bmatrix}
1 & 0 & t_{x} \\
0 & 1 & t_{y} \\
0 & 0 & 1 \\
\end{bmatrix} 
\begin{bmatrix}
x \\
y \\1
\end{bmatrix} $

이처럼 3x3 변환행렬로 변경되어야 변환이 가능하다.

2. 다양한 변환

 

3. Matrix Composition

여러 변환을 하나의 행렬곱으로 표현할 수 있다.
아래와 같은 예시를 보면 회전변환, 스케일링, Translation을 행렬곱을 통해 적용하는 것을 볼 수 있다.
$\begin{bmatrix}x'\\ y'\\1\end{bmatrix}=
\begin{bmatrix}1 & 0 & t_{x} \\0 & 1 & t_{y} \\0 & 0 & 1 \\\end{bmatrix} 
\begin{bmatrix}a & 0 & 0 \\0 & b & 0 \\0 & 0 & 1 \\\end{bmatrix} 
\begin{bmatrix}\cos\theta & -\sin\theta & 0 \\\sin\theta &\cos\theta & 0 \\0&0&1\end{bmatrix} 
\begin{bmatrix}x \\y \\1\end{bmatrix} $

회전변환 행렬(2차원, 3차원)

2차원에서 회전 변환 행렬은 다음과 같다. 

• $R(\theta)=\begin{bmatrix}
  \cos\theta & -\sin\theta \\
  \sin\theta &\cos\theta \\
  \end{bmatrix} $
• 각도 $\theta$ 만큼 반시계 방향으로 회전한다고 생각할 수 있다.
  혹은 $ e_{1} = \begin{pmatrix} 1\\0 \end{pmatrix} e_{2}= \begin{pmatrix} 0\\1 \end{pmatrix} $ 가 이동한다고 생각하는 것이 더 좋아보인다.

증명

3차원에서의 회전 변환 행렬

• 2차원 회전과는 다르게 회전 방향을 다양하게 하여 회전할 수 있다.
  즉 회전축이 다양하다.
  • x축 기준 회전
    $R_{x}(\theta)=\begin{bmatrix}
     1&0  &0  \\
     0& \cos\theta & -\sin\theta \\
     0& \sin\theta & \cos\theta \\
    \end{bmatrix}$
    
    
  • y축 기준 회전
    $R_{y}(\theta)= \begin{bmatrix}
     \cos\theta& 0 & \sin\theta \\
    0 & 1 & 0 \\
    -\sin\theta & 0 & \cos\theta \\
    \end{bmatrix}$
    
    
  • z축 기준 회전
    $R_{z}(\theta)= \begin{bmatrix}
    \cos\theta & -\sin\theta & 0 \\
     \sin\theta& \cos\theta & 0 \\
     0& 0 & 1 \\
    \end{bmatrix} $

2차원 회전행렬에서 파생된 것으로 직관적으로 이해할 수 있는데,
기준이 되는 축의 값이 변하지 않도록 되어있다.

좌표계 변환

한 공간에서 취할 수 있는 기저는 다양하다. 때문에 문제에 따라 알맞은 basis를 취하여 쉬운 문제로 만들 수 있다.

$\mathbb{R}^{2}$에서 $\mathbf{x}=\begin{bmatrix}4\\-2 \end{bmatrix}$를 다른 basis B: $\mathbf{b}_{1} =\begin{bmatrix} 1 \\ -1 \end{bmatrix}, \mathbf{b}_{2} =\begin{bmatrix} 1 \\ 1 \end{bmatrix}$ 를 사용한다면 다른 좌표로 나타날 것이다. 
$ [\mathbf{x}]_{\mathbf{B}}=\begin{bmatrix}3\\1 \end{bmatrix} $ 로 좌표가 바뀌었지만 같은 벡터이다.

변환 방법은 $\begin{bmatrix}1 & 1 \\ -1 & 1 \\ \end{bmatrix} 
\begin{bmatrix} x_{1} \\x_{2} \end{bmatrix} = 
\begin{bmatrix} 4 \\ -2 \end{bmatrix} $ 에서 $x_{1},x_{2}$ 를 구하여 B 좌표계로 변환할 수 있다.

좌표계변환 행렬은 일반적인 변환행렬의 역이라고 할 수 있다.
직관적으로 보자면 일반적인 변환 행렬은 좌표를 옮기지만 좌표계를 옮기게 되면 본래 좌표가 반대로 이동하는 것처럼 보인다.
이것이 바로 역행렬로 변환이 수행되는 것이다.