티스토리 뷰
선형대수
1. 벡터(Vector)
벡터는 크기와 방향을 가지고 있는 양을 나타내는 개념이다. 주로 물리학에서 힘이나 속도 등을 나타낼 때 사용되지만, 선형대수학에서는 여러 숫자들을 일렬로 나열한 형태로 나타낼 수 있다. 벡터는 일반적으로 **열 벡터(column vector)**나 **행 벡터(row vector)**로 표현된다.
- 행 벡터(row vector): $\mathbf{v} = [v_{1}, v_{2}, ..., v_{n}]$ (크기 1 x n)
- 열 벡터(column vector): $\mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix}$ (크기 n x 1)
- 벡터에는 차원이 있으며 벡터 성분의 개수를 의미한다.
2. 행렬(Matrix)
행렬은 숫자들을 직사각형 형태로 배열한 것이다. 각 원소들은 벡터들의 결합으로 볼 수 있으며, 주로 벡터 변환이나 시스템의 방정식을 풀 때 사용된다.
- 행 은 가로방향 열은 세로방향을 나타낸다.
- 행렬의 크기는 행과 열의 수로 정의된다. 예를 들어, 2x3 행렬은 2개의 행과 3개의 열을 갖는다.
+ 행렬을 표현하는 방식이 많다(선형대수에서) 때문에 논문을 봤을 때도 이게 어떤 행렬이구나 판단할 수 있어야 한다.
예를들어 벡터로 구성된 행렬은 벡터 리스트로만 보이는경우도 있기에 ...
3. Linear Space (선형공간)
선형공간은 벡터들로 이루어진 집합으로, 두 가지 주요 조건을 만족해야 한다:
- 벡터 덧셈: 두 벡터를 더한 결과가 또 다른 벡터가 된다.
- 스칼라 곱: 벡터에 숫자(스칼라)를 곱한 결과가 또 다른 벡터가 된다.
즉, 선형공간은 벡터 덧셈과 스칼라 곱이 가능한 벡터들의 집합이다. 예를 들어,$\mathbb{R}^{n}$ 은 n차원의 실수 벡터들이 이루는 선형공간이다.
4. 선형결합 (Linear Combination)
선형결합은 여러 벡터들을 특정한 상수(스칼라)로 곱한 후 더한 것이다. 예를 들어, 벡터 $\mathbf{v}_{1}, \mathbf{v}_{2}, \dots, \mathbf{v}_{k}$에 대해 스칼라 $c_1, c_2, \dots, c_k$가 주어지면, 그들의 선형결합은 다음과 같다:
$c_{1} \mathbf{v}_{1} + c_{2} \mathbf{v}_{2} + \dots + c_{k} \mathbf{v}_{k}$
선형결합은 벡터들이 어떻게 조합될 수 있는지 보여준다.
예를들어 $\mathbb{R}^{2}$ 상의 임의의 point는 $\mathbf{v}_{1}, \mathbf{v}_{2}$ 의 linear combination으로 표현할 수 있다.
5. 선형독립 (Linear Independence)
벡터들이 선형독립이라면, 어떤 벡터도 나머지 벡터들의 선형결합으로 나타낼 수 없다는 의미이다.
반대로 하나의 벡터가 다른 벡터의 linear combination으로 표현된다면 선형종속이다.
예를 들어, 벡터 $\mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_k$가 선형독립이라면, 이 벡터들의 선형결합이 0 벡터가 되는 유일한 방법은 모든 스칼라가 0일 때뿐이다.
벡터들이 선형 독립이고 Matrix $A=[ \mathbf{v}_1 \ \mathbf{v}_2 \dots \mathbf{v}_k] $ 일때
Ax=0 형태에서 trivial solution 만을 가진다.
non-trivial solution 이라면 dependent하다.
free variable이 있으면 non-trivial sol이 존재하고 때문에 dependent 함을 알 수 있다.
free variable은 피봇이 없는 column의 variable을 의미한다.
6. 행렬의 곱 (Matrix Multiplication)
행렬의 곱셈은 두 행렬을 결합하는 연산이다. 행렬 곱셈은 스칼라 곱과 덧셈을 결합한 것으로, 다음과 같이 정의된다.
행렬 A가 m×n 크기이고, 행렬 B가 n×p 크기일 때, 두 행렬 A와 B의 곱 AB는 m×p 크기의 행렬이 된다. 이때 각 원소는 A의 행과 B의 열을 곱한 값들의 합으로 계산된다.
예를 들어, 행렬 $A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$와 $B = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix}$ 일 때, AB는:
$AB = \begin{bmatrix} 1*5 + 2*7 & 1*6 + 2*8 \\ 3*5 + 4*7 & 3*6 + 4*8 \end{bmatrix} = \begin{bmatrix} 19 & 22 \\ 43 & 50 \end{bmatrix}$
7. 역행렬 (Inverse Matrix)과 항등행렬 (Identity Matrix)
- 역행렬(Inverse matrix): 어떤 행렬 A에 대해, $A^{-1}$는 다음 조건을 만족하는 행렬이다:
$A \cdot A^{-1} = A^{-1} \cdot A = I$
정방행렬에 대해 행렬곱 결과가 항등행렬이 된다.
여기서 $\ I $는 항등행렬(Identity matrix). - 항등행렬(Identity matrix): $\ I $는 모든 대각선 원소가 1이고, 나머지 원소가 0인 정사각행렬.
예를 들어, 2x2 항등행렬은:$I=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$
항등행렬은 어떤 행렬과 곱할 때, 원래 행렬이 변하지 않는 특성을 가진다.
8. 정방행렬 (Square Matrix)
정방행렬은 행과 열의 수가 같은 행렬이다.
예를 들어, 2x2, 3x3, 4x4 등과 같은 행렬들이 정방행렬이다.
정방행렬은 역행렬, 행렬식(determinant) 등 다양한 특성을 가지고 있다.
9. 대각행렬 (Diagonal Matrix)
대각행렬은 주대각선(왼쪽 위에서 오른쪽 아래로 가는 대각선) 외의 모든 원소가 0인 행렬이다.
예를 들어, 3x3 대각행렬은 다음과 같다:
$D = \begin{bmatrix} d_1 & 0 & 0 \\ 0 & d_2 & 0 \\ 0 & 0 & d_3 \end{bmatrix}$
10. 전치행렬 (Transpose)
- 전치행렬은 행과 열을 서로 바꾼 행렬이다.
- 행렬 A의 전치행렬은 $A^{T}$로 표기하며, A의 i-번째 행을 $A^{T}$의 i-번째 열로 바꾸는 것이다.
예를 들어, 행렬 $A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$의 전치행렬은:
$A^{T} = \begin{bmatrix} 1 & 3 \\ 2 & 4 \end{bmatrix}$ - 때문에 n x m 크기 행렬의 전치행렬은 m x n 크기이다.
- 전치행렬은 다음 특징을 가진다.
1. $(A^{T})^{T} = A$
2. $(A+B)^{T}=A^{T}+B^{T}$
3. scalar 값 r에 대하여 $(rA)^{T} = rA^{T}$
4. $(AB)^{T} = B^{T}A^{T}$
11. Span과 Basis
- Span: 벡터 집합이 생성하는 공간을 말한다. 예를 들어, 두 벡터 $\mathbf{v}_{1}$과 $\mathbf{v}_{2}$가 있으면, 이 두 벡터의 선형결합으로 생성될 수 있는 모든 벡터들의 집합이 바로 그 벡터들의 span이다.
- Basis: 벡터 공간에서 벡터 집합이 해당 공간을 생성하며, 동시에 선형독립인 벡터들의 집합을 basis(기저)라고 한다. 즉, 벡터 공간을 나타내는 최소한의 선형독립적인 벡터 집합을 basis라고 한다. 예를 들어, $\mathbb{R}^{3}$의 basis는 3개의 선형독립적인 벡터로 구성된다.
basis 벡터의 linear combination으로 벡터공간 내의 모든 벡터를 생성할 수 있다.
+ 선형대수에서 중요한 개념,, 여러 성질을 가지고 있고 .. linear transform 했을 경우에도 등등...
linear transform
$\mathbf{x} \boldsymbol{x} \mathit{x}$
n차원 벡터$ \mathbf{x} \boldsymbol{x} \mathit{x} $ mxn 행렬 A를 곱하면 m차원 벡터가 얻어진다. 행렬A로 인해 다른 벡터로 옮기는 변환이 결정된 것이다. 단순한 하나의 예시로는 점을 점으로 옮기는 이미지가 연상되지만 공간이 행렬로 인해 어떻게 변하는지 떠올려야한다.
$A=\begin{pmatrix} 1&-0.3\\0.7&0.6 \end{pmatrix}$ 와 같은 행렬에 의해 공간이 어떻게 변하는지 떠올리기 위해서는
다음과 같이 생각할 수 있다.
$e_{1} = \begin{pmatrix} 1\\0 \end{pmatrix} e_{2}= \begin{pmatrix} 0\\1 \end{pmatrix} $ 을 각각
$\begin{pmatrix} 1\\-0.7 \end{pmatrix}$와 $\begin{pmatrix} -0.3\\0.6 \end{pmatrix}$ 로 이동시킨다.
행렬의 곱도 이처럼 이해할 수 있다. $\boldsymbol{x}$를 A를 이용해 $\boldsymbol{y}$로 변환한다.
이를 B를 이용해 $\boldsymbol{z}$로 변환한다.
이 과정을 행렬곱 BA를 이용해 한번에 z로 변환하는 것이다.
Ax=b 에 대한 해석도 두 가지로 볼 수 있다.
1. A column들에 대한 linear combination으로 b가 만들어진다.
2. A에 의해 x가 b로 transform 된다.
행렬 A(mxn)에 의한 transform은 $T : \mathbb{R}^{n} \to \mathbb{R}^{m}$
Linear Transformation의 조건은 다음과 같다.
---
때문에 T(x)=Ax로 표현되는 것은 모두 Linear Transform이다.
x가 T로 인해 T(x)가 되었고
이를 다른 좌표에서 보면 어떨까?
2D Transformation
위치를 평면이동하는
translation에 회전까지 고려한 Euclidean
scale까지 고려한 similarity
변형이되었지만 평행이 유지가 된 affine 변환
투영과 관련된 projective 변환 이 있다.
1. Translation
크기, 각도, 면적을 유지하며 위치만 이동하는 경우이다.
x' = x + t_{x}
y' = y+t_{y}
translation을 2x2 행렬 M으로 표현하기에는 문제가 따르며
이를 해결하기 위해서는 homogeneous 좌표계가 필요하다.
성분 1을 추가하여 3차원 형태로 나타난다.
회전변환 행렬(2차원, 3차원)
2차원에서 회전 변환 행렬은 다음과 같다.
- $R(\theta)=\begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta &\cos\theta \\
\end{bmatrix} $ - 각도 $\theta$ 만큼 반시계 방향으로 회전한다고 생각할 수 있다.
혹은 $ e_{1} = \begin{pmatrix} 1\\0 \end{pmatrix} e_{2}= \begin{pmatrix} 0\\1 \end{pmatrix} $ 가 이동한다고 생각하는 것이 더 좋아보인다.
증명

좌표계 변환
한 공간에서 취할 수 있는 기저는 다양하다. 때문에 문제에 따라 알맞은 basis를 취하여 쉬운 문제로 만들 수 있다.
$\mathbb{R}^{2}$에서 $\mathbf{x}=\begin{bmatrix}4\\-2 \end{bmatrix}$를 다른 basis $B=\mathbf{b}_{1} =\begin{bmatrix} 1 \\ -1 \end{bmatrix}, \mathbf{b}_{2} =\begin{bmatrix} 1 \\ 1 \end{bmatrix}$ 를 사용한다면 다른 좌표로 나타날 것이다.
$ [\mathbf{x}]_{\mathbf{B}}=\begin{bmatrix}3\\1 \end{bmatrix} $ 로 좌표가 바뀌었지만 같은 벡터이다.
확률과 통계
1. 확률변수의 정의
sample space 랜덤하게 나온 확률값을 가진...
하나하나의 outcome에 sample space의 실수를 대응
X(w) 가 x에 매핑이 된다. x에 해당하는 값이 확률 변수이다.
- 확률을 함수처럼 다루기 위해 확률을 집합의 문제를 숫자의 문제로 만들면서 생긴 개념.
- P(event) 를 P(x) 로 다룰 수 있도록 특정 event에 대응하는 실수인 확률 변수를 만듦.
- 확률변수는 함수의 변수가 되는 실수
- 랜덤한 형태로 나오는 outcome을 특정한 실수에 대응하여 얻어지는 것이 x
ex) 동전을 던질 때 확률변수의 정의
임의로 앞면은 1, 뒷면은 0처럼 정의할 수 있음.
그렇다면 P(앞면) = P(1) = 1/2
1은 앞면이라는 event에 대응하는 숫자(=특정한 outcome에 대응하는 숫자)
2. 결합확률과 조건부확률
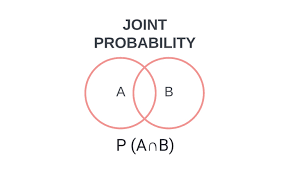
- 결합확률 $P(B \cap A)$ : A와 B 사건이 동시에 발생할 확률
- 조건부확률: $P(B|A)$: $P(B|A)=\frac{P(B ∩ A)}{P(A)}$
A가 발생할 확률에서 A와 B가 동시에 발생할 확률과 같음.
3. Total Probability
- 어떤 사건 A가 상호 배타적인(mutually exclusive) 사건 $B_{1}, B_{2}, \ldots, B_{n}$ 에 의해 발생할 수 있을 때 P(A)는 다음과 같다.
$P(A) = \sum_{i=1}^{n} P(A | B_{i}) \cdot P(B_{i})$
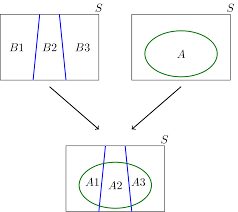
- $P(A) = P(A_{1})+ P(A_{2})+... P(A_{n})$ 일때
$P(A_{1}) = P(B_{1} \cap A)$ 이고
$= P(B_{1}) P(A|B_{1}) $ 이라 할 수 있다.
조건부확률에서 $P(A|B_{i}) = \frac{P(A \cap B_{i})}{ P(B_{i})} $ 이므로
$P(A \cap B_{i}) = P (A|B_{i}) \cdot P (B_{i}) $ 이다.
- 즉 $P(A) = \sum_{i=1}^{n}P(B_{i})P(A|B_{i})$ 이다.
4. 베이즈 정리
두 확률변수의 사전확률과 사후확률 사이의 관계를 나타내는 정리이다.
사전확률로 사후 확률을 구할 수 있다.
- 조건부 확률에서 $P(B|A)=\frac{P(B\cap A)}{P(A)}$ 임을 알고 있다.
- 즉 $P(B \cap A) = P(B|A)P(A)$ 이다. 아래 식에 대입하면
- $P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{P(B|A)P(A)}{P(B)} $ 이다.
- 분모 P(B)는 다음과 같이 구할 수 있다.
$P(B) = P(B|A)P(A)+P(B|A_{c})P(A_{c})$
- 분모 P(B)는 다음과 같이 구할 수 있다.
베이즈 정리 예제
- 60% 확률로 거짓말을 하는 사람, 90% 정확도를 가진 거짓말 탐지기
사전확률 P(A) : 거짓말을 할 확률, 사전확률 P(B) : 거짓말 탐지기에서 양성이 뜰 확률 - 탐지기가 거짓이라 판정했을 때 실제로 거짓일 확률을 구해보자: P(A|B)
우선 P(B) 는 전체확률의 법칙을 이용하여 구하면- $P(B)= P(B|A)P(A)+P(B|A_{c})P(A_{c}) = 0.9*0.6+0.1*0.4=0.58$
- 다음 P(A|B)를 구하면
- $P(A|B) = \frac{P(B|A)P(A)}{P(B)} = 0.9*0.6/0.58 \approx 0.9310$
5. 독립사건
- 사건 A와 B가 독립이면
$P(B|A) = P(B)$ 이고 $P(A|B)=P(A)$ 이다. - 독립(independent)과 상호배타적(mutually exclusive=배반사건?)인 것은 다르다.
6.Expectation(mean) 과 분산
산술평균은 보통 x1+x2+ ... xn / N
각 변수별로 event의 수(w1, w2, w3, ,,, wn) 가 다르다면 평균은 다음과 같음
$\frac{w1x1+w2x2 +... + wnxn }{w1+w2+ ... + wn}$
- $E[X] =\sum_{i} x_{i}P(x_{i})$
- 만약 연속확률변수일 경우에는
$= \int_{-\infty}^{\infty}xf_{x}(x)dx$
그래프를 상상해보면 x근처의 dx라는 작은 폭을 갖는 막대, 이를 적분하여 평균을 얻음
expectation 예제
- k가 발생할 확률이 다음과 같을 때
$P_{k}(k)=\frac{\lambda^{k}}{k!}\cdot e^{-\lambda}, k=0,1,2,\cdots $ - $E[K]=\sum_{k=0}^{\infty} k\cdot \frac{\lambda^{k}}{k!}\cdot e^{-\lambda}$
- 테일러 급수: $f(x) = \frac{f^{(0)}(0)}{0!} x^{0} + \frac{f^{(1)}(0)}{1!} x^{1} + \cdots$
- $E[K]= \sum_{k=1}^{\infty} \frac{\lambda \cdot \lambda^{k-1}}{(k-1)!}\cdot e^{-\lambda} $
$=\lambda e^{-\lambda}\sum_{k=1}^{\infty} \frac{\lambda^{k-1}}{(k-1)!} = \lambda$
Moments
n차 moment
$E[X^{n}] = \sum x_{i}^{n}P(x_{i}) = \int_{-\infty}^{\infty} x^{n}f_{x}(x)dx$
n=1 이면 Expectation(mean) $E[X] (=\mu) $
Central Moments
- X라는 변수에서 u라는 평균을 빼고 n제곱하여 평균낸 것
- $E[(X-\mu )^{n}]
= \sum (x_{i}-\mu)^{n}P(x_{i})
= \int (x-\mu)^{n}f_{x}(x)dx$
- n=1 의 경우
$E[X-\mu] = \int (x-\mu)f_{x}(x)dx = \int xf_{x}(x)dx - \mu \int f_{x}(x)dx = \mu-\mu = 0$ - n=2의 경우
$E[(X-\mu)^{2}] = \sigma_{X}^{2} = $ Variance 분산
분산
$Var(X) = \sigma_{X}^{2} = E[(X-\mu)^{2}] $
$=E[x^{2}-2x \mu + \mu ^{2}] = E[X^{2}] - 2\mu E[X]^{2} + \mu^{2}$
$= E[X^{2}] - \mu^{2}$
$=E[X^{2}] - E[X]^{2}$
expectation 연산은 Linear 하다. (homogeniety & superposition)
실수곱, x1+x2 일치 f(ax1+bx2) = af(x1)+bf(x2)
1. 확률변수
- 확률변수는 무작위 실험의 결과를 수치로 표현한 것입니다.
- 이산 확률변수: 값이 특정한 정수 집합에 속함 (예: 주사위 눈 1~6).
- 연속 확률변수: 값이 연속적인 범위에서 나옴 (예: 특정 시간 동안의 온도).
2. 독립사건
- 두 사건 A와 B가 독립적이라는 것은, 한 사건의 발생이 다른 사건의 발생에 아무런 영향을 미치지 않는다는 의미입니다.
- 수학적으로: P(A∩B)=P(A)⋅P(B)
3. 결합확률과 조건부확률
- 결합확률 P(A∩B) $P(A \cap B)$ : 두 사건 A와 B가 동시에 발생할 확률.
- 조건부확률 P(A∣B) : 사건 B가 발생했을 때, 사건 A가 발생할 확률.
$P(A | B) = \frac{P(A \cap B)}{P(B)} \quad (P(B) \neq 0)$ - 사건 A와 B가 독립적일 경우: P(A∣B)=P(A) (B가 발생했든 안 했든 A의 확률은 동일함.)
4. 베이즈 정리
- 조건부확률을 계산할 때 사용하는 매우 중요한 법칙: $P(A | B) = \frac{P(B | A) \cdot P(A)}{P(B)}$
- 인공지능에서 사후확률을 구하거나, 데이터를 기반으로 예측할 때 자주 사용됨.
5. 전체확률의 정리
- 어떤 사건 B가 여러 상호 배타적인 사건 $A_{1}, A_{2}, \ldots, A_{n}$에 의해 발생할 수 있을 때, B의 확률은 이렇게 계산한다: $P(B) = \sum_{i=1}^{n} P(B | A_{i}) \cdot P(A_{i}) $
$A_{1}, A_{2}, \ldots, A_{n}$
$P(B) = \sum_{i=1}^{n} P(B | A_{i}) \cdot P(A_{i})$
6. 기대값과 분산
- 기대값 E[X]: 확률변수가 가질 수 있는 값들의 평균적인 기대치.
$E[X] = \sum_{x} x \cdot P(X=x) \quad (\text{이산형})$
$E[X] = \int_{-\infty}^\infty x \cdot f(x) dx \quad (\text{연속형})$ - 분산 $\text{Var}(X)$: 확률변수가 평균으로부터 얼마나 퍼져 있는지 측정.
$Var(X)=E[(X−E[X])^{2}]=E[X^{2}]−(E[X])^{2}$
'전기전자공학 > 수학' 카테고리의 다른 글
| 행렬식과 Eigenvalue & Eigenvector (0) | 2025.03.05 |
|---|---|
| [선형대수] Linear Transformation (0) | 2025.02.11 |
| [선형대수] Gram-Schmidt process와 QR 분해 (0) | 2025.02.10 |
| [수학] 자연성장, 감소/로지스틱 방정식 (0) | 2020.05.31 |
| [수학] 미분방정식, 방향장, 오일러 방법 (0) | 2020.05.31 |
| [수학] 리만합과 근삿값 (0) | 2020.05.31 |
| [수학] 특이적분 (0) | 2020.05.31 |
| [수학] 삼각함수와 적분 (0) | 2020.05.31 |
- Total
- Today
- Yesterday
- 계산방법
- 카시오
- 문서 스캔
- 북문
- 타란튤라
- 리브모바일
- f-91w
- 시계 줄
- 파스타
- Liiv M
- 알뜰 요금제
- 10만포인트
- 배송기간
- 리브엠
- 알뜰폰요금제
- 할인
- f-94w
- 티스토리챌린지
- 맛집
- mealy
- 방어동작
- a모바일
- 교체
- 오블완
- 카카오페이
- 경북대
- 알리익스프레스
- 네이버페이
- 메쉬 밴드
- 방향장
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
