티스토리 뷰
matrix로 그래프 구현하기
행 정점에서 열 정점(vertext)으로 가는 길(edge)이 있다면 1로, 없다면 0으로 구현하려고 한다.
무방향 그래프라면 행렬이 대칭으로 나타날 것이다.
그래프는 구조체로 선언하고 내부에 정점의 개수와 2차원 배열을 멤버 변수로 선언할 것이다.
typedef struct GraphType {
int n; // 정점의 개수
int adj_mat[MAX_VERTICES][MAX_VERTICES];
} GraphType;필요한 함수
- init
- insert_vertex
- insert_edge
- print_adj_mat
함수 설명
1) init
// 그래프 초기화
void init(GraphType* g)
{
int r, c;
g->n = 0;
for (r = 0; r<MAX_VERTICES; r++)
for (c = 0; c<MAX_VERTICES; c++)
g->adj_mat[r][c] = 0;
}이중 반복으로 행렬을 0으로 채웠다.
2) insert_vertex
// 정점 삽입 연산
void insert_vertex(GraphType* g, int v)
{
if (((g->n) + 1) > MAX_VERTICES) {
fprintf(stderr, "그래프: 정점의 개수 초과");
return;
}
g->n++;
}정수 v 정점을 받고 GraphType 구조체의 정점 개수 n을 증가시켜 준다.
3) insert_edge
void insert_edge(GraphType* g, int start, int end)
{
if (start >= g->n || end >= g->n) {
fprintf(stderr, "그래프: 정점 번호 오류");
return;
}
g->adj_mat[start][end] = 1;
g->adj_mat[end][start] = 1;
}
4) print_adj_mat
void print_adj_mat(GraphType* g)
{
for (int i = 0; i < g->n; i++) {
for (int j = 0; j < g->n; j++) {
printf("%2d ", g->adj_mat[i][j]);
}
printf("\n");
}
}5) main 함수
void main()
{
GraphType *g;
g = (GraphType *)malloc(sizeof(GraphType));
init(g);
for(int i=0;i<4;i++)
insert_vertex(g, i);
insert_edge(g, 0, 1);
insert_edge(g, 0, 2);
insert_edge(g, 0, 3);
insert_edge(g, 1, 2);
insert_edge(g, 2, 3);
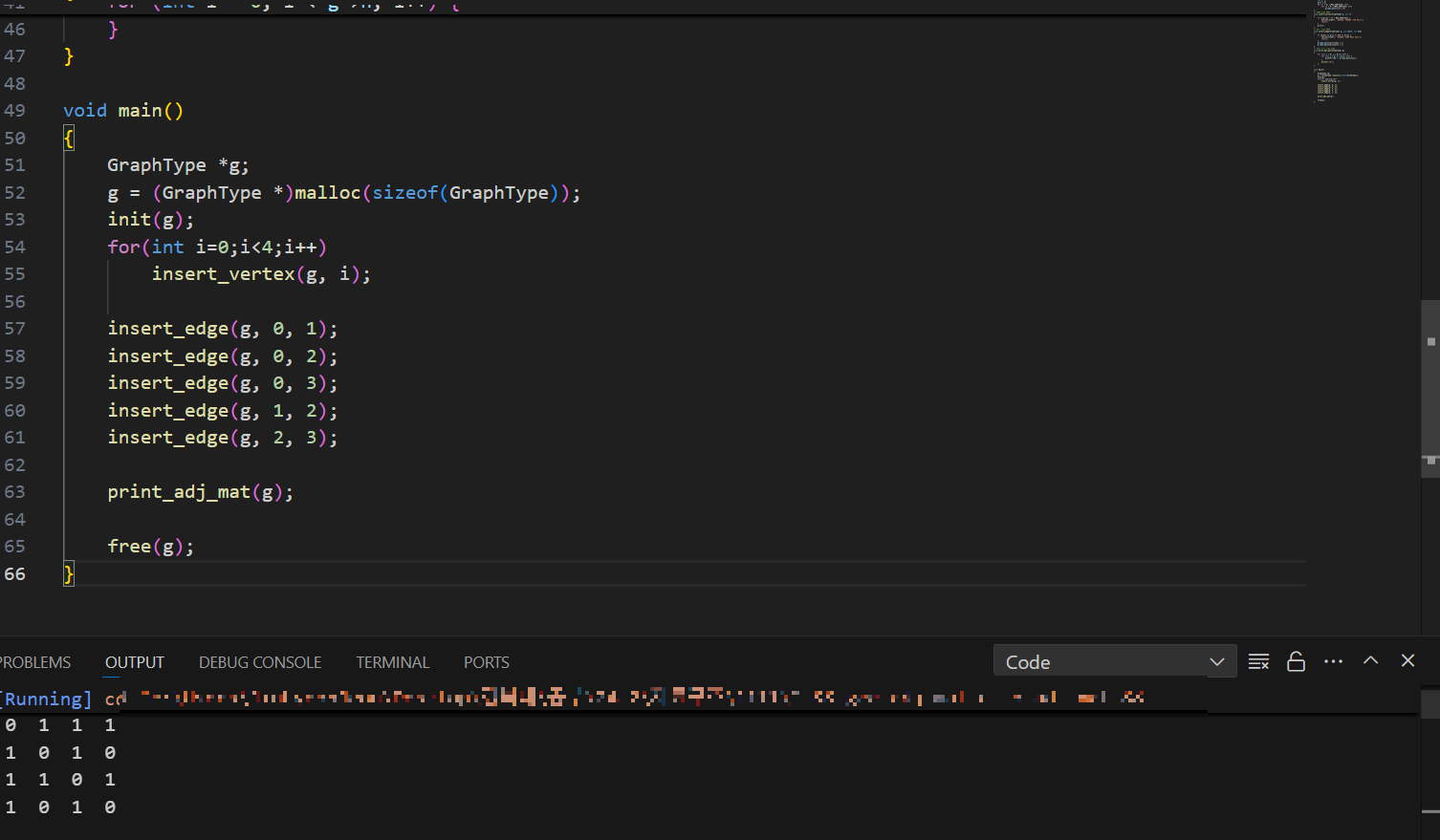
print_adj_mat(g);
free(g);
}GraphType 구조체를 포인터형으로 선언하고 메모리를 할당했다.
insert_vertex 함수를 이용해 0에서 4까지 정점을 만든다.
그리고 insert_edge 함수로 정점 사이에 간선(edge)을 만들어준다.
마지막으로 출력함수를 이용해 2차원 배열을 출력한다.
연결리스트로 그래프 구현하기
GraphNode 구조체와 GraphType 구조체를 선언할 것이다.
GraphType 에는 정점의 개수 n과 GraphNode 포인터형의 리스트가 있다.
typedef struct GraphNode{
int vertex;
struct GraphNode* link;
} GraphNode;
typedef struct GraphType {
int n; // 정점의 개수
GraphNode* adj_list[MAX_VERTICES];
} GraphType;GraphType에 있는 n은 정점의 개수를 가리키고, adj_list는 그래프노드를 가리킬 것이다.
필요한 함수
- init
- insert_vertex
- insert_edge
- print_adj_list
함수 설명
1) init
void init(GraphType* g)
{
int v;
g->n = 0;
for (v = 0; v<MAX_VERTICES; v++)
g->adj_list[v] = NULL;
}정점의 개수 n을 0으로 업데이트 한 뒤 adj_list 배열의 값을 전부 NULL로 바꾸었다.
2) insert_vertex
void insert_vertex(GraphType* g, int v)
{
if (((g->n) + 1) > MAX_VERTICES) {
fprintf(stderr, "그래프: 정점의 개수 초과");
return;
}
g->n++;
}정수 v 정점을 받고 GraphType 구조체의 정점 개수 n을 증가시켜 준다.
3) insert_edge
void insert_edge(GraphType* g, int u, int v){
GraphNode* node;
if (u >= g->n || v >= g->n) {
fprintf(stderr, "그래프: 정점 번호 오류");
return;
}
node = (GraphNode*)malloc(sizeof(GraphNode));
node->vertex = v;
node->link = g->adj_list[u];
g->adj_list[u] = node;
}새로운 노드를 만들고 메모리를 할당한 뒤 adj_list가 node를 가리키도록 한다. 즉 배열 바로 뒤에 노드를 추가하는 것이다.
4) print_adj_list
void print_adj_list(GraphType* g) {
for (int i = 0; i<g->n; i++) {
GraphNode* p = g->adj_list[i];
printf("정점 %d의 인접 리스트 ", i);
while (p!=NULL) {
printf("-> %d ", p->vertex);
p = p->link;
}
printf("\n");
}
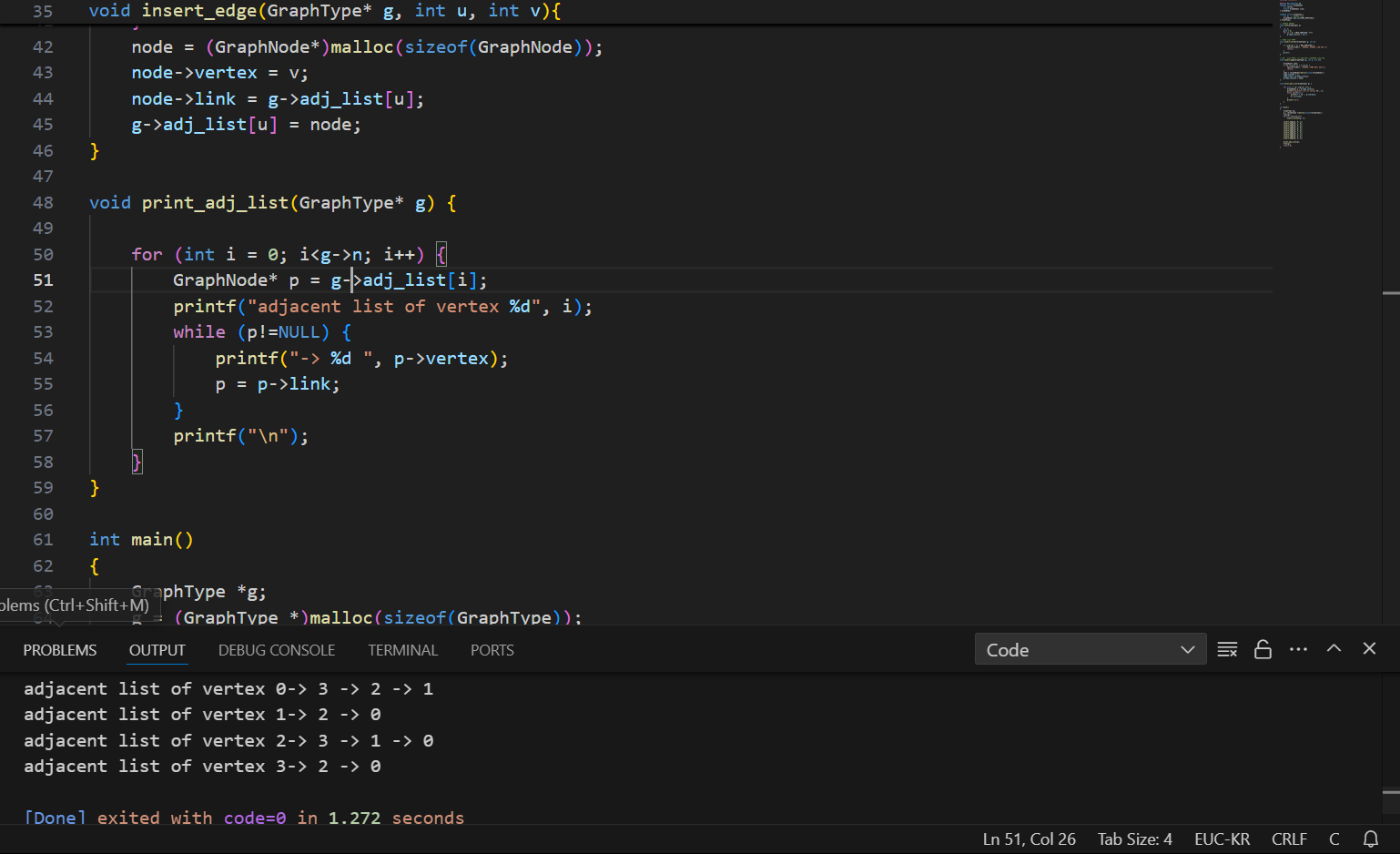
}adj_list를 순회하며 NULL이 아닐때까지 돌아가며 출력한다.
5) main 함수
int main()
{
GraphType *g;
g = (GraphType *)malloc(sizeof(GraphType));
init(g);
for(int i=0;i<4;i++)
insert_vertex(g, i);
insert_edge(g, 0, 1);
insert_edge(g, 1, 0);
insert_edge(g, 0, 2);
insert_edge(g, 2, 0);
insert_edge(g, 0, 3);
insert_edge(g, 3, 0);
insert_edge(g, 1, 2);
insert_edge(g, 2, 1);
insert_edge(g, 2, 3);
insert_edge(g, 3, 2);
print_adj_list(g);
free(g);
return 0;
}GraphType 구조체를 포인터형으로 선언하고 메모리를 할당했다.
insert_vertex 함수를 이용해 0에서 4까지 정점을 만든다.
그리고 insert_edge 함수로 정점 사이에 간선(edge)을 만들어준다.
마지막으로 출력함수를 이용해 연결리스트로 구성된 그래프를 출력한다.
'Computer Science > CS & data' 카테고리의 다른 글
| [컴퓨터구조] RISC-V 파이프라인 data/control hazards (0) | 2024.11.24 |
|---|---|
| C언어 spanning tree(신장트리)와 MST 구현 방법 (0) | 2024.11.21 |
| C언어 그래프에서 DFS와 BFS 구현 (탐색) (0) | 2024.11.20 |
| C언어 이진 탐색 트리 BST 구현하기 (0) | 2024.11.19 |
| ROS2 파이썬을 이용한 topic subscribe, publish (0) | 2024.11.07 |
| S32K144 MCU Keil v5 프로젝트 생성 방법 (0) | 2024.10.10 |
| ROS2 기본 구조와 패키지 (0) | 2024.10.03 |
| 미니콘다 & 주피터 노트북 (파이썬) 설치 | 가상환경 설정 (0) | 2024.09.10 |
- Total
- Today
- Yesterday
- 무어머신
- 10만포인트
- 문서 스캔
- 티스토리챌린지
- Liiv M
- 할인
- 네이버페이
- 맛집
- 교체
- 메쉬 밴드
- 방향장
- mealy
- 파스타
- f-94w
- 시계 줄
- 알리익스프레스
- 알뜰폰요금제
- 오블완
- f-91w
- 계산방법
- 카카오페이
- 배송기간
- 리브엠
- 카시오
- 북문
- 경북대
- 알뜰 요금제
- 밀리머신
- a모바일
- 리브모바일
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
