티스토리 뷰
[물리전자] PN junction Forward Bias에서 캐리어 농도 (Excess Carrier Concentration)
흔한 학생 2023. 12. 4. 03:28
이번 장에서는 Forward Bias에서 Carrier injection
Continuity Equation과 Diffusion Equation으로 캐리어 농도의 일반해를 구하고
Depletion edge의 소수캐리어 농도를 구해 경계 조건을 구한 후
최종적으로 Excess carrier 농도 식을 구해보겠습니다.
Forward Bias에서 Carrier Injection
우선 가정을 합니다.
1) Steady state
2) Nondegenerately uniformly doped 1-D step junction
3) Low level injection in the quasi-neutral region
(minority carrier concentration << majority carrier concentration)
4) No other processes other than drift, diffusion, and thermal recombinationgeneration
때문에 $np$는 다음과 같이 나타낼 수 있습니다.
$np=n_{i}^{2}e^{qV/kT}$
-Law of junction
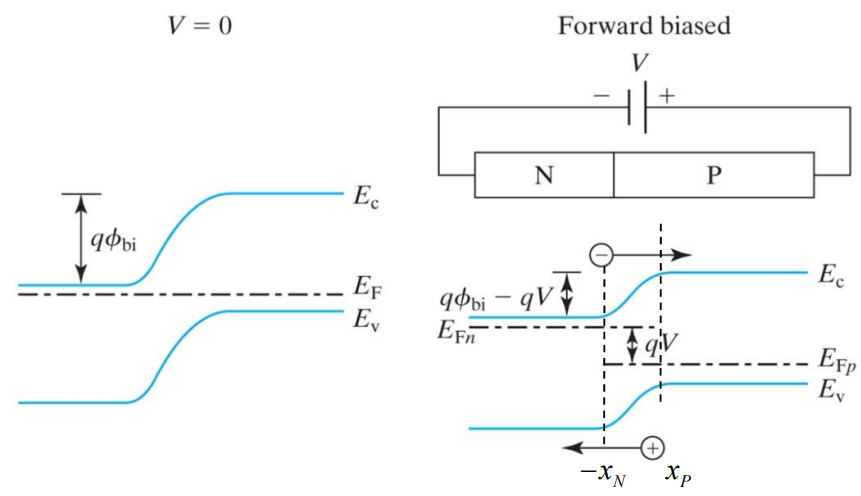
유도방법
DC bias에서 quasi-Fermi level을 이용해 n과 p를 정의했었습니다.
$n=N_{C}e^{-(E_{C}-E_{Fn})/kT}$
$p=N_{V}e^{-(E_{Fp}-E_{V})/kT}$
$$np=N_{C}e^{-(E_{C}-E_{Fn})/kT}N_{V}e^{-(E_{Fp}-E_{V})/kT}$$
$$=N_{C}N_{V}e^{-(E_{C}-E_{V})/kT}e^{(E_{Fn}-E_{Fp})/kT}$$
에너지밴드 diagram에서 쉽게 볼 수 있듯이
$E_{Fn} - E_{Fp} = qV$ 이기 때문에 다음과 같은 결과가 나옵니다.
Forward bias 상황에서 np는 $n_{i}^{2}$보다 큼을 알 수 있습니다.
Continuity Equation
전류가 흐르는 공간을 생각해봅시다.

이때 박스에서 carrier 변화는 다음과 같습니다.
캐리어 변화 = 들어오는 캐리어 - 나가는 캐리어 - 박스 내부에서 재결합하는 캐리어 + 내부에서 생성되는 캐리어
이를 식으로 정리하면 캐리어 변화에 대한 미분방정식을 얻을 수 있습니다.
$\frac{\partial p(x,t)}{\partial t}=-\frac{1}{q}\frac{dJ_{P}(x)}{dx}-\frac{p'}{\tau_{p}}$
이를 carrier에 대한 Continuity equation 이라 합니다.
Diffusion Equation
minority carrier current에 대해서 diffusion current가 지배적이라 할 수 있습니다.
$J=-qD_{p}\frac{dp}{dx}$ , $J=qD_{n}\frac{dn}{dx}$
diffusion이 지배적이기에
이전에 배운 diffusion 전류 밀도 식을 continuity equation에 대입해주면
$\frac{d^{2}p'}{dx^{2}}=\frac{p'}{D_{p}\tau_{p}}=\frac{p'}{L_{p}^{2}}$
$L_{p}=\sqrt{D_{p}\tau_{p}}$
$\frac{d^{2}n'}{dx^{2}}=\frac{n'}{D_{n}\tau_{n}}=\frac{n'}{L_{n}^{2}}$
$L_{n}=\sqrt{D_{n}\tau_{n}}$
이렇게 도출된 식을 diffusion equation 이라 합니다.
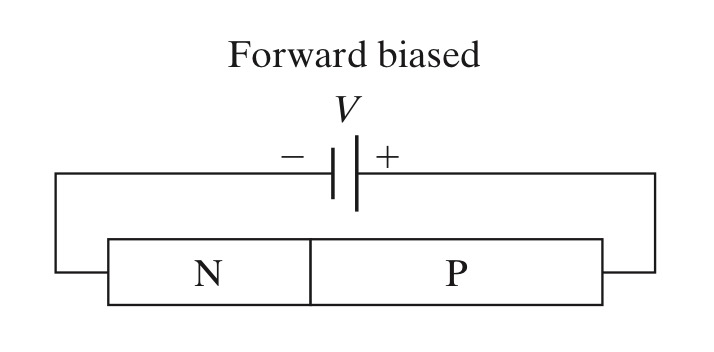
이 내용을 Forward bias 상황에서도 적용할 수 있습니다.
기존 식에서 V는 built-in potential $V_{bi}$를 의미한 것이었다면Forward bias $V_{a}$를 가한 상황에서는 V 자리에 $V_{bi}-V_{a}$ 를 대입해주면 될 것입니다.
이로서 평형 상태와 Forward bias 상황의depletion edge $x_{P}$ $-x_{N}$에서의 소수 캐리어 농도를 알 수 있었습니다.
Excess Carriers in Forward Biased PN junction
공핍 영역의 edge에서의 값만 구해봤는데요.
그렇다면 공핍영역 이후 영역에 대한 Excess Carrier 에 대한 농도 식 또한 구해봅시다.
diffusion equation의 일반해를 구해보면 이와 같이 나옵니다.
$p'(x)=Ae^{x/L_{p}}+Be^{-x/L_{p}}$
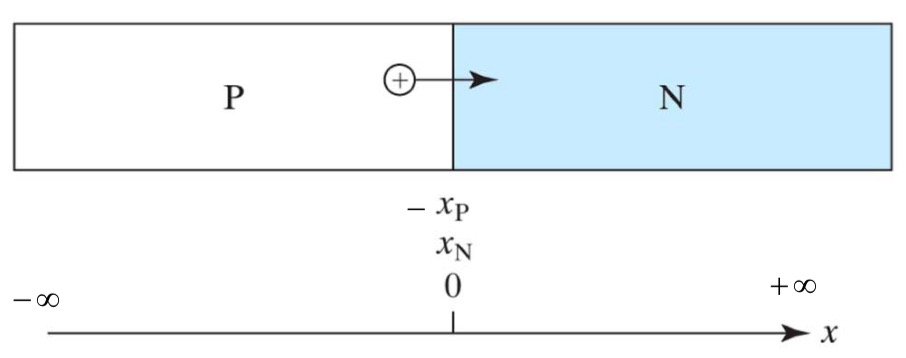
Boundary Condition
식을 완성하기 위해 경계 조건을 구해봅시다.
1. $x_{N}$, $-x_{P}$
edge ($x_{N}$ 와 $-x_{P}$)에서의 값을 구해봅시다.
depletion edge 에서 소수 캐리어 농도
(minority carrier concentration)
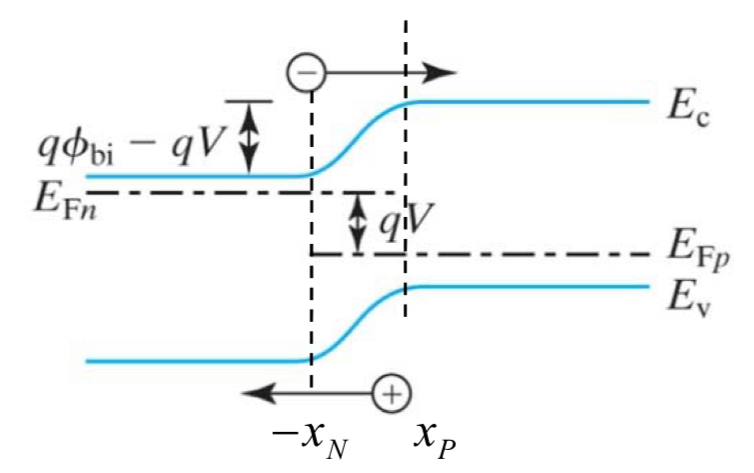
공핍영역의 경계에서 캐리어 농도는 어떻게 구할 수 있을까요?
우선 depletion 영역과 P-type의 경계 지점을 $x_{p}$,
그리고 N-type과 경계 지점을 $-x_{N}$ 이라 합시다.
$np=n_{i}^{2}e^{qV/kT}$ 임을 알았고
P-type 에서의 소수 캐리어 농도는 다음과 같이 나타낼 수 있습니다.
유도
$n(x_{P})= \frac{n_{i}^{2}}{p(x_{P})}e^{qV/kT}=\frac{n_{P}p_{P}}{p(x_{P})}e^{qV/kT}$ 입니다.
여기서 $p_{P}=p(x_{P})$ 이므로 다음과 같은 결과가 나옵니다.
$n_{P}e^{qV/kT}=\frac{n_{i}^{2}}{N_{a}}e^{qV/kT}$
$n(x_{P})=n_{P}e^{qV/kT}=\frac{n_{i}^{2}}{N_{a}}e^{qV/kT}$
마찬가지로 N-type에서 소수 캐리어 농도를 구해보면
$p(-x_{N})=p_{N}e^{qV/kT}=\frac{n_{i}^{2}}{N_{d}}e^{qV/kT}$
이렇게 구한 소수캐리어의 경계 값을 Quasi Equilibrium Boundary Condition
혹은 Shockley Boundary Condition 이라 합니다.
depletion edge excess carrier concentration
바로 위에서 depletion edge에서 소수캐리어 농도를 구했습니다.
그렇다면 excess 캐리어 농도를 바로 알 수 있는데요.
그 이유는 이미 소수 캐리어 농도를 $n_{P}$ $p_{N}$ 으로 잡았기 때문에
기존 소수 캐리어 농도를 제거해 excess 캐리어 농도를 구할 수 있습니다.
$n'(x_{P})=n_{P}(e^{qV/kT}-1)$
$p'(-x_{N})=p_{N}(e^{qV/kT}-1)$
이는 Excess carrier에 대한 quasi equilibrium boundary condition 이라 할 수 있겠습니다.
이처럼 경계에서 excess carrier는
V와 기존 소수캐리어 농도 n, p 에 의해 결정이 됩니다.
2. $\infty$
그리고 무한대로 멀어진다면
소수캐리어 농도 n'과 p'은 0으로 수렴할 것입니다.
1번과 2번 두 경계조건을 대입해주면 다음과 같은 결론이 나옵니다.
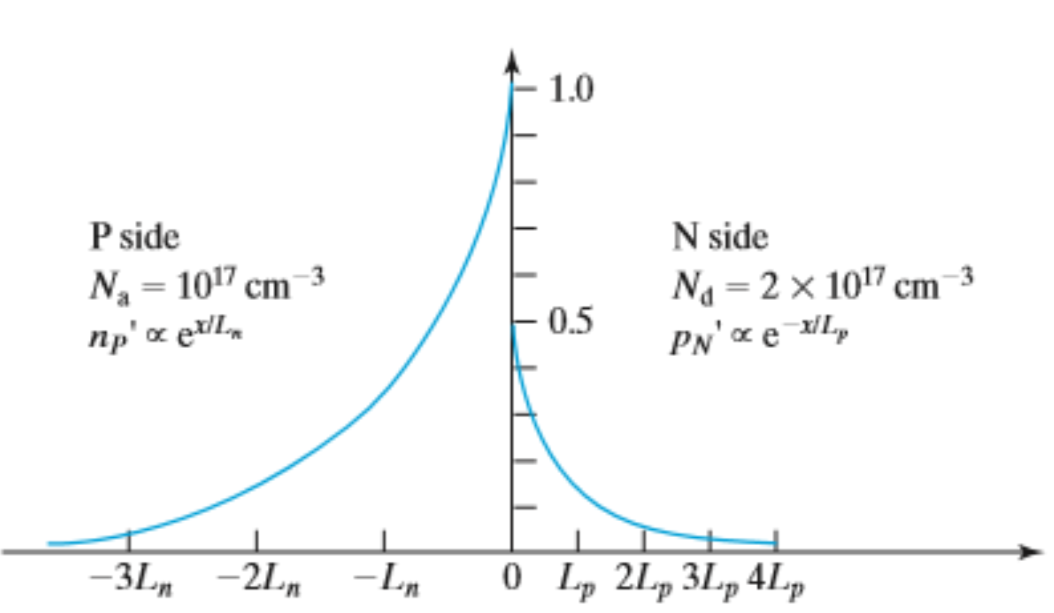
N side
$$p'(x)= p_{N}(e^{qV/kT}-1)e^{-(x-x_{N})/L_{p}}, (x>x_{N})$$
P side
$$n'(x)= n_{P}(e^{qV/kT}-1)e^{(x+x_{P})/L_{n}}, (x<-x_{P}) $$
이렇게 나온 Excess Carrier 에 대한 식은 앞으로 문제를 풀 때 유용하게 쓰일 예정이니
꼭 기억해두시길 바랍니다.
[물리전자] PN 다이오드 I-V 특성, Ideal & Real 다이오드 전류 특성
전 글에서 Excess (minority) carrier 에 대한 식을 도출해냈습니다. 이전글 [물리전자] Forward Bias에서 캐리어 농도, Continuity Equation, Diffusion Equation, Excess carrier 이번 장에서는 Forward Bias에서 Carrier injection
studentstory.tistory.com
'전기전자공학 > 반도체 소자 공학 (물리전자|전자소자)' 카테고리의 다른 글
| [전자소자] MOS 밴드 다이어그램(for gate Voltage) (0) | 2024.03.11 |
|---|---|
| [전자소자] MOS Capacitor Flat-Band Condition (1) | 2024.03.06 |
| [물리전자] PN 다이오드 I-V 특성, Ideal & Real 다이오드 전류 특성 (0) | 2023.12.17 |
| [물리전자] PN Junction depletion 영역 (Width, Capacitance) (1) | 2023.12.17 |
| [물리전자] 이상적인 다이오드 원리 설명 (1) | 2023.12.04 |
| GIFET (gate injection based field effect transistor)소자란? (0) | 2023.12.02 |
| [물리전자] Junction breakdown [Tenneling(Field Ionization), Avalanche (Impact Ionization)] (1) | 2023.12.01 |
| [물리전자] PN Junction Built-in Potential (1) | 2023.12.01 |
- Total
- Today
- Yesterday
- 무어머신
- 카카오페이
- mealy
- 방향장
- 알리익스프레스
- 교체
- 배송기간
- 카시오
- 메쉬 밴드
- f-91w
- 리브엠
- 알뜰폰요금제
- 문서 스캔
- f-94w
- 리브모바일
- 파스타
- 네이버페이
- 10만포인트
- a모바일
- 알뜰 요금제
- 경북대
- Liiv M
- 맛집
- 할인
- 밀리머신
- 시계 줄
- 북문
- 티스토리챌린지
- 계산방법
- 오블완
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
