티스토리 뷰
[물리전자] PN Junction depletion 영역 (Width, Capacitance)
흔한 학생 2023. 12. 17. 15:04
[물리전자] PN Junction Built-in Potential
N과 P의 접합을 만들어봅시다. 접합을 만드는 방법에는 두 가지 방법이 있습니다? 첫 번째로는 확산을 이용하는 방법이 있고 두 번째로는 implantation 방법이 있습니다.? (implantiation은 ) 이때 기존 P
studentstory.tistory.com
Depletion-Layer Model

공핍 영역의 크기는 어떻게 될까요?
우선 전기장은 모든 곳에서 연속적이어야 하며
공핍영역의 끝에서는 0일 것입니다.
이 경계조건을 이용해 알아보겠습니다.
P영역 경계에서
$\frac{dE}{dx}=-\frac{qN_{a}}{\varepsilon_{s}}$
$E(x)= -\frac{qN_{a}}{\varepsilon_{s}}x+C_{1}$
$=\frac{qN_{a}}{\varepsilon_{s}}(x_{P}-x)$
similarly N side
$E(x)=$
$\frac{qN_{d}}{\varepsilon_{s}}(x+x_{N})$
$N_{a}x_{P}=N_{d}x_{N}$
다음 Potential 또한 공핍영역의 끝에서 0이어야 하므로
P영역
$V(x)=-\int E(x)dx + D$
$=\frac{qN_{a}}{\varepsilon_{s}}(-x_{P}x+\frac{1}{2} x^{2})+D$
$=\frac{qN_{a}}{\varepsilon_{s}}(x_{P}-x)^{2}$
N영역
$V(x)=-\int E(x)dx + D$
$=\phi_{bi}-\frac{qN_{d}}{\varepsilon_{s}}(x-x_{N})^{2}$
depletion-layer width
이렇게 나온 전압 V 식에서 x=0에서 연속이어야 하므로
P영역, N영역의 V(0)이 같음을 이용해 식을 정리합니다.
그리고 Naxp = NdxN 식을 연립하면 공핍 영역 너비 식이 나옵니다.

폭 $W_{dep}= x_{P}p+x_{N} = \frac{2\varepsilon_{s}\phi _{bi}}{q}(\frac{1}{N_{a}}+\frac{1}{N_{d}}) $
즉 도핑 농도가 작은 것에 더 의존적입니다.
one sided junction

만약 Doner의 농도가 훨씬 낮은 $N_{a} >> N_{d}$라면
$\frac{1}{N_{a}}$ 는 무시할 수 있고
결국 W는 $W_{dep}=\sqrt{\frac{2\varepsilon_{s}(\phi _{bi}+V_{r})}{qN}}$ 으로 일반화 할 수 있습니다.
Reverse-Biased PN Junction
reverse bias에서 depletion 영역은 확장됩니다.
기존에 depletion영역의 폭을 설명하는 식을 유도해보았는데요.
인가된 전압으로 인해 $V_{r}$이 추가됩니다.
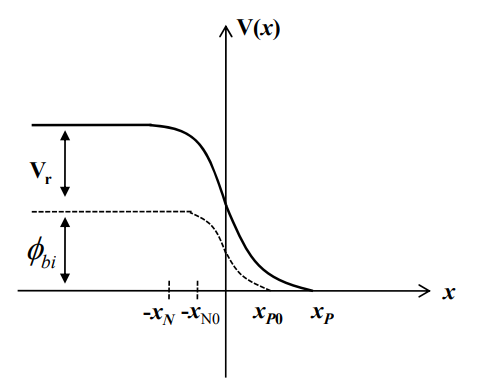
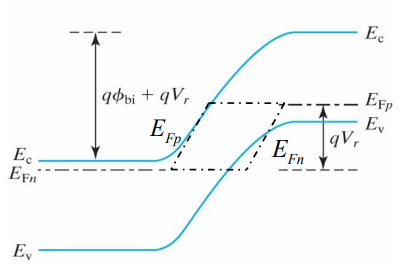
때문에 장벽은 built-in potential과 전압의 합으로 나타나게 됩니다.
$$q(\phi _{bi}+V_{r})$$
Capacitance - Voltage Characteristics (C - V 특성)
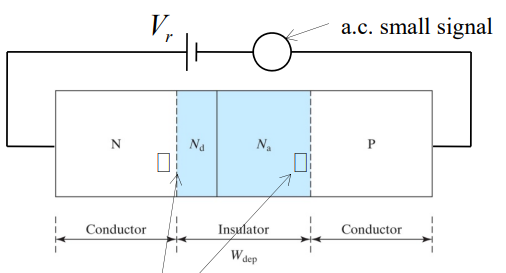
Depletion 영역으로 인해 커패시터처럼 charge가 축적됩니다.
이때 커패시턴스 C는 다음과 같이 나타납니다.
$C=A\frac{\varepsilon_{s}}{W}$
그렇다면 PN junction에서 커패시턴스 $C_{dep}$ 도 나타낼 수 있을겁니다.
이때 Width W는 이전에 구한 식에서 다음과 같이 유도되었습니다.
$W_{dep}=\sqrt{\frac{2\varepsilon_{s}(\phi _{bi}+V_{r})}{qN}}$
대입해보면 depletion-layer capacitance를 구할 수 있습니다.
$$\frac{1}{C_{dep}^{2}} = \frac{2(\phi_{bi}+V_{r})}{qN\varepsilon_{s}A^{2}}$$
Junction Breakdown
PN junction에는 Breakdown이 존재합니다.
이상적인 다이오드라면 reverse bias 영역에서 전류가 흐르지 않습니다.
하지만 실제로는 과도한 역방향 전압이 걸려 breakdown voltage를 넘는다면
역방향으로 급격한 전류가 흐르게 됩니다.
Breakdown에서는 Avalanching Process / Zener Process 두 과정이 존재하는데요.
제너 다이오드는 Breakdown 영역을 사용하도록 설계되었습ㄴ디ㅏ..
Peak Electric Field
PN junction 다이오드 전기장 피크치를 넘어섰을 때 Breakdown이 발생합니다.
다음 N+ P junction을 예로 봅시다.
이때 doner가 더 많고 one sided junction 이기 때문에 Na로만 판정.
전기장 E는 ~~라 할 수 있다.
breakdown voltage를 $V_{B}$라 하고 대입하면
Peak Electric Field 는 다음과 같이 나온다.
또한 이때의 breakdown voltage는
$V_{B}=\frac{\varepsilon_{s}E_{crit}^{2}}{2qN}-\phi _{bi}$ 이다.
[물리전자] Avalanche Breakdown (Impact Ionization)
이전 글에서는 Breakdown의 두 가지 프로세스 중 Tunneling (Zener Process)에 대해 알아봤습니다. 이번에는 두 번째 Avalanche Breakdown에 대해 알아보겠습니다. Avalanche Breakdown 이전 zener Process 에서는 전기장
studentstory.tistory.com
'전기전자공학 > 반도체 소자 공학 (물리전자|전자소자)' 카테고리의 다른 글
| [전자소자] MOS게이트 전압 Vg(for depletion, threshold, inversion) (0) | 2024.03.13 |
|---|---|
| [전자소자] MOS 밴드 다이어그램(for gate Voltage) (0) | 2024.03.11 |
| [전자소자] MOS Capacitor Flat-Band Condition (1) | 2024.03.06 |
| [물리전자] PN 다이오드 I-V 특성, Ideal & Real 다이오드 전류 특성 (0) | 2023.12.17 |
| [물리전자] PN junction Forward Bias에서 캐리어 농도 (Excess Carrier Concentration) (0) | 2023.12.04 |
| [물리전자] 이상적인 다이오드 원리 설명 (1) | 2023.12.04 |
| GIFET (gate injection based field effect transistor)소자란? (0) | 2023.12.02 |
| [물리전자] Junction breakdown [Tenneling(Field Ionization), Avalanche (Impact Ionization)] (1) | 2023.12.01 |
- Total
- Today
- Yesterday
- 리브엠
- 교체
- 북문
- Liiv M
- 카카오페이
- f-91w
- a모바일
- 알뜰폰요금제
- 티스토리챌린지
- 문서 스캔
- f-94w
- 경북대
- 방향장
- 네이버페이
- 계산방법
- 파스타
- 밀리머신
- 할인
- 오블완
- 카시오
- 리브모바일
- 메쉬 밴드
- 배송기간
- 시계 줄
- 맛집
- mealy
- 알리익스프레스
- 알뜰 요금제
- 무어머신
- 10만포인트
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
