티스토리 뷰
[전자장] 파의 반사와 투과 (Normal incident)
이전 시간에 전기장과 자기장의 비 $\eta$ 에 대해 알아보았습니다. $$E=\eta H$$ $\eta$ 는 굴절률 비와 반대입니다. 전기장과 자기장이 입사할 때 반사와 투과가 어떻게 되는지 알아보려고 합니다. 우
studentstory.tistory.com
Oblique incident
반사면에 수직으로 입사하는 것이 아닌 비스듬히 입사하는 파를 살펴보겠습니다.

아시다시피 전기장과 자기장은 서로 수직으로 진행합니다.
이전 글에서는 전기장과 자기장 모두 반사면에 수직으로 입사하는 경우였습니다.
비스듬히 입사하는 경우를 따로 공부하는 이유는?
수직으로 입사하는 Normal incident와 무엇이 다르기에 따로 공부하는 것일까요?
자기장과 전기장이 수직으로 진행하는데
그 방향에 따라 달라질 수 밖에 없습니다!
비스듬히 입사할 때는 경우가 두 가지로 나뉩니다.
하나는 전기장이 입사면에 수직이거나 다른 하나는 자기장이 입사면에 수직입니다.
단순히 말로만 하면 이해가 잘 안될텐데요.
그림으로 보여드리겠습니다.
Perpendicular polarization
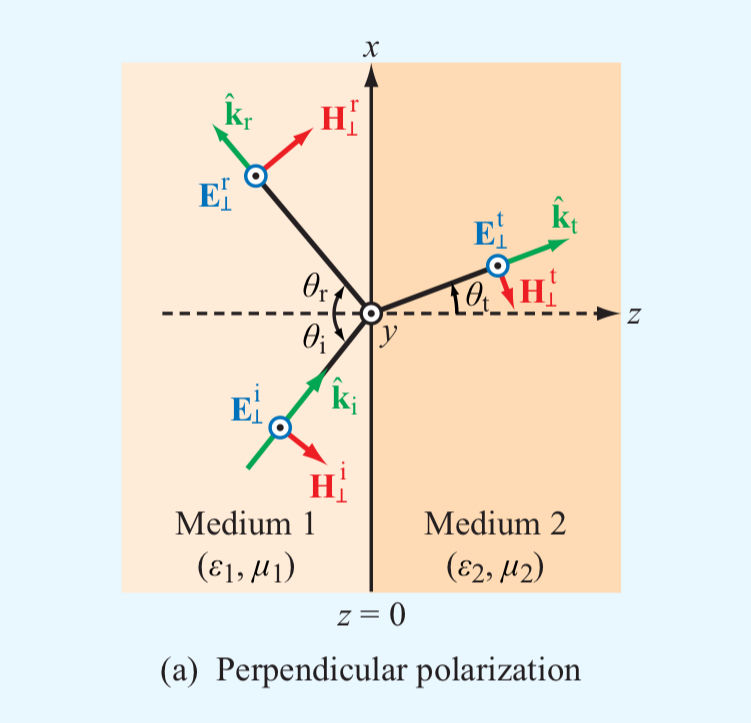
전기장이 입사면에 perpendicular, 즉 수직인 경우입니다.
전기장이 입사면을 가로지른다 하여
Transverse electric (TE)
라고도 부릅니다.
Parallel polarization
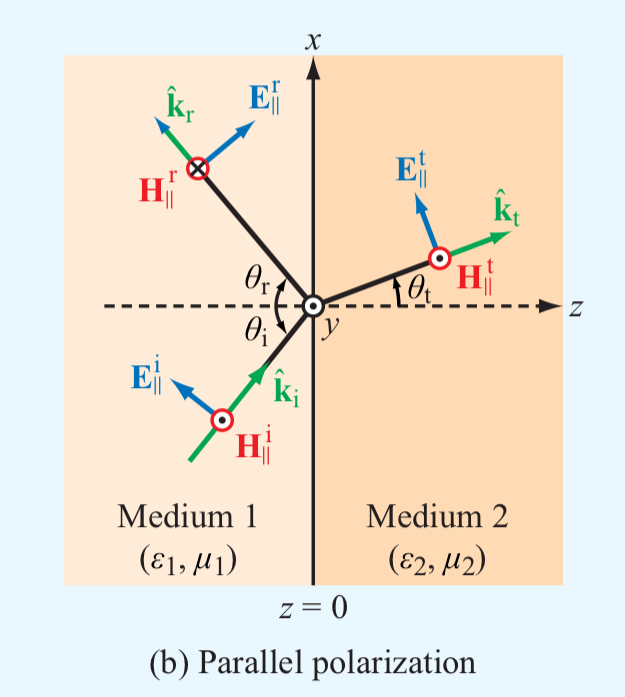
전기장이 입사면에 parallel, 평행한 경우입니다.
즉 자기장이 입사면에 수직이겠죠?
자기장이 입사면을 가로지른다 하여
Transverse magnetic (TM)
라고도 부릅니다.
두 가지 경우에서 입사면에 수직인 성분(TE에서 전기장, TM에서 자기장)은 이전 글과 다를 게 없습니다.
문제가 되는 것은 수직이 아닌 성분입니다.
그림을 보면서 설명드리겠습니다.
이전에 배운 전기장과 자기장의 Boundary condition을 떠올려야 하는데요.
전기장이 입사면에 수직인 TE의 경우
입사각을 $\theta_{i}$ 굴절각을 $\theta_{t}$ 로 했습니다.
자기장을 반사면에 수직인 성분과 평행한 성분으로 나누어 볼 수 있겠죠?
이때 평행한 성분만으로 반사계수와 투과계수를 알아낼 수 있습니다!
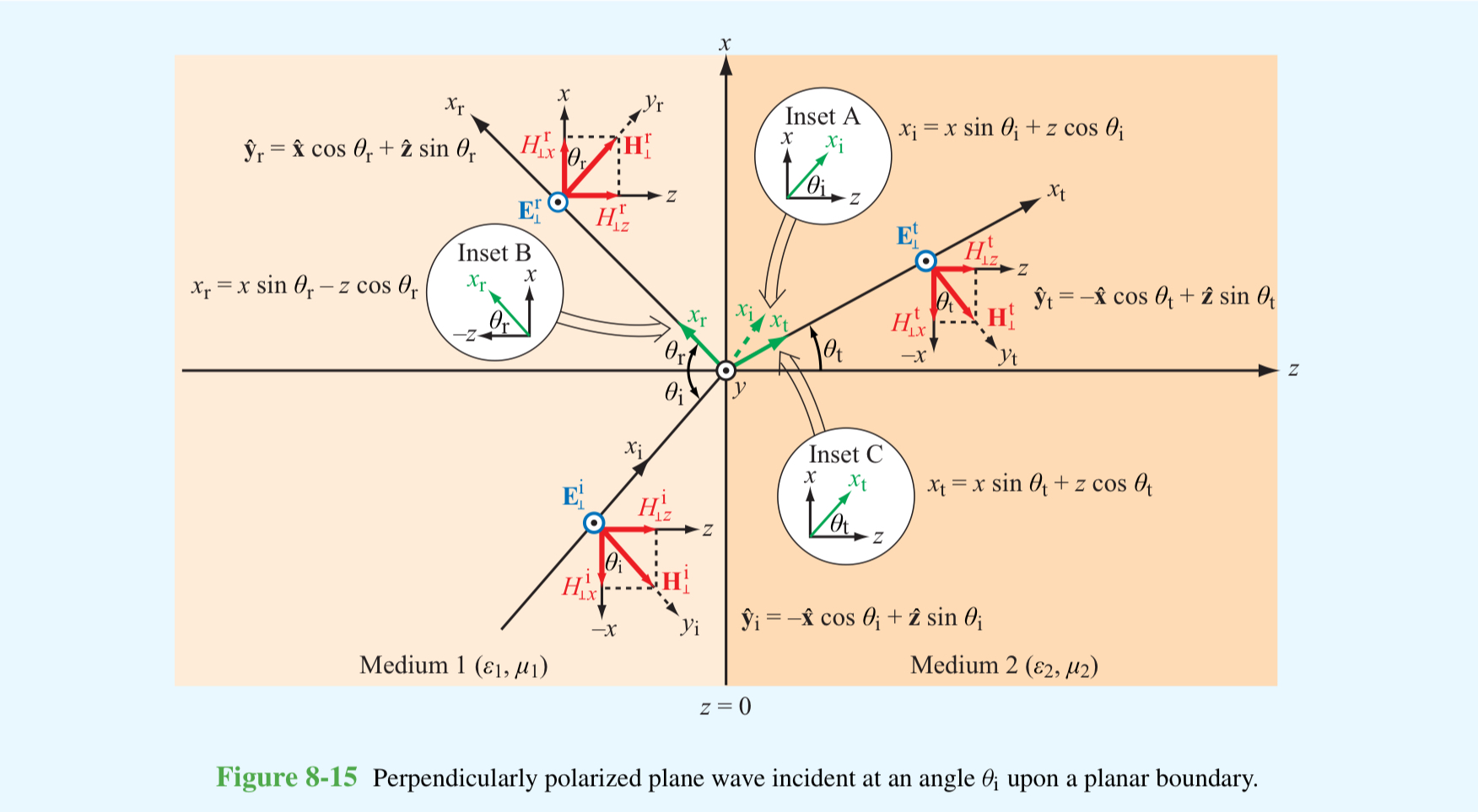
평행한 성분의 크기
| 입사 | 반사 | 투과 |
| $cos\theta_{i}$ | $cos\theta_{i}$ | $cos\theta_{t}$ |
$$A+B=C$$
$$\frac{cos\theta_{i}}{\eta_{1}}(A-B)=\frac{cos\theta_{t}}{\eta_{2}}$$
반사계수를 구해보면
$$\Gamma=\frac{\eta_{2}cos\theta_{i}-\eta_{1}cos\theta_{t}}{\eta_{2}cos\theta_{i}+\eta_{1}cos\theta_{t}}$$
유도방법 (야매)
$\Gamma = \frac{\eta_{2}- \eta_{1} }{ \eta_{2} + \eta_{1} }$ 이었으니
$\eta_{1}$ 에 $\frac{\eta_{1}}{cos\theta_{i}}$ 대입
$\eta_{2}$ 에 $\frac{\eta_{2}}{cos\theta_{t}}$ 대입
투과계수를 구해보면
$$\tau=\frac{C}{A}=\frac{2\eta_{2}cos\theta_{i}}{ \eta_{2}cos\theta_{i}+\eta_{1}cos\theta_{t} }$$
유도방법
$\tau = \Gamma +1$
자기장이 입사면에 수직인 TM 의 경우
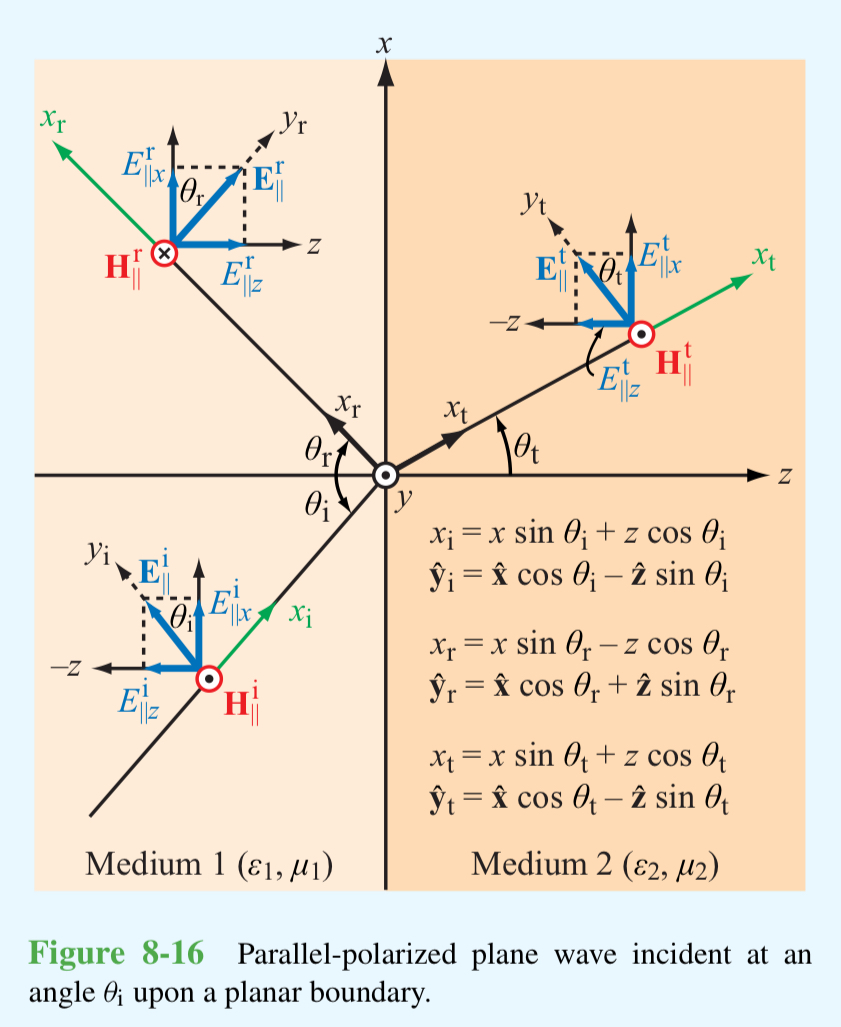
평행한 성분의 크기
| 입사 | 반사 | 투과 |
| $cos\theta_{i}$ | $cos\theta_{i}$ | $cos\theta_{t}$ |
$$cos\theta_{i}(A+B)=cos\theta_{t}C$$
$\frac{1}{\eta_{}}$
반사계수를 구해보면
$$\Gamma=\frac{\eta_{2}cos\theta_{i}-\eta_{1}cos\theta_{t}}{\eta_{2}cos\theta_{t}+\eta_{1}cos\theta_{i}}$$
유도방법
$A(1-\frac{\eta_{2}cos\theta_{t}}{\eta_{1}cos\theta_{i}})=-B(1+\frac{\eta_{2}cos\theta_{t}}{\eta_{1}cos\theta_{i}})$
투과계수를 구해보면
$$\tau=\frac{C}{A}=\frac{2\eta_{2}cos\theta_{i}}{ \eta_{2}cos\theta_{t}+\eta_{1}cos\theta_{i} }$$
유도방법
$\tau=(1+\Gamma)\frac{cos\theta_{i}}{cos\theta_{t}}$
사진의 출처는 PEARSON에 있습니다.
[전자장] 브루스터 각 (Brewster angle)
이전 시간까지 Nomal, Oblique incident 에서 전기장과 자기장의 반사, 투과에 대해 알아봤습니다. 입사각에 따라 반사계수 $\Gamma$와 투과계수 $\tau$가 달라지는데요. 이 값들은 0이 될 수 있을까요? 결
studentstory.tistory.com
'전기전자공학 > 전자공학' 카테고리의 다른 글
| [전자장] 전송선 envelope, Partial standing waves 부분 정상파 (0) | 2023.12.14 |
|---|---|
| [전자장] 광도파로 (Waveguide) - Effective wavelength 파장 (0) | 2023.12.13 |
| [전자장] Transmission Lines 전송선의 정의와 기본 구성 (0) | 2023.11.26 |
| [전자장] 전자기파의 밀도: 포인팅 벡터 (0) | 2023.11.15 |
| [전자장] 브루스터 각 (Brewster angle) (1) | 2023.11.06 |
| [전자장] 파의 반사와 투과 (Normal incident) (0) | 2023.11.06 |
| [논리회로] Finite State Machine - FSM moore, mealy machine (무어 밀리 머신) (2) | 2023.07.16 |
| ulaby fundamentals of Applied Electromagnetics 솔루션 (0) | 2023.06.04 |
- Total
- Today
- Yesterday
- 파스타
- 오블완
- 문서 스캔
- 시계 줄
- f-94w
- 카카오페이
- 리브모바일
- 밀리머신
- 계산방법
- 무어머신
- 메쉬 밴드
- 네이버페이
- f-91w
- mealy
- 북문
- 알뜰 요금제
- 알리익스프레스
- Liiv M
- 카시오
- 알뜰폰요금제
- 배송기간
- 방향장
- 경북대
- 맛집
- a모바일
- 티스토리챌린지
- 교체
- 리브엠
- 10만포인트
- 할인
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
