[전자장] Transmission Lines 전송선의 정의와 기본 구성

 

 

전송선이란 송신단의 전원회로와 수신단의 부하를 연결하는 4단자 회로망을 말합니다.
회로에서 도선을 무시하곤 했는데 항상 무시해도 될까요? 
- 항상 그렇진 않습니다.
위상차가 발생합니다
 

Dispersion

전송선에는 dispersion 즉 분산이 존재합니다.
구형파를 생각해보면 구형파는 여러 주파수 sin파의 합으로 볼 수 있습니다.
(푸리에 급수로 알아낼 수 있습니다)

dispersive line을 거치면 속도 변화가 생기고
속도 변화는 주파수마다 다릅니다.
때문에 선을 거친 신호에는 왜곡이 발생합니다.

빛의 분산과 같이 생각하면 쉬운데
빛이 다른 매질로 진행할 때 파장에 따라 속도가 달라지고 굴절이 일어나죠.
마찬가지입니다.
 

전송선의 종류

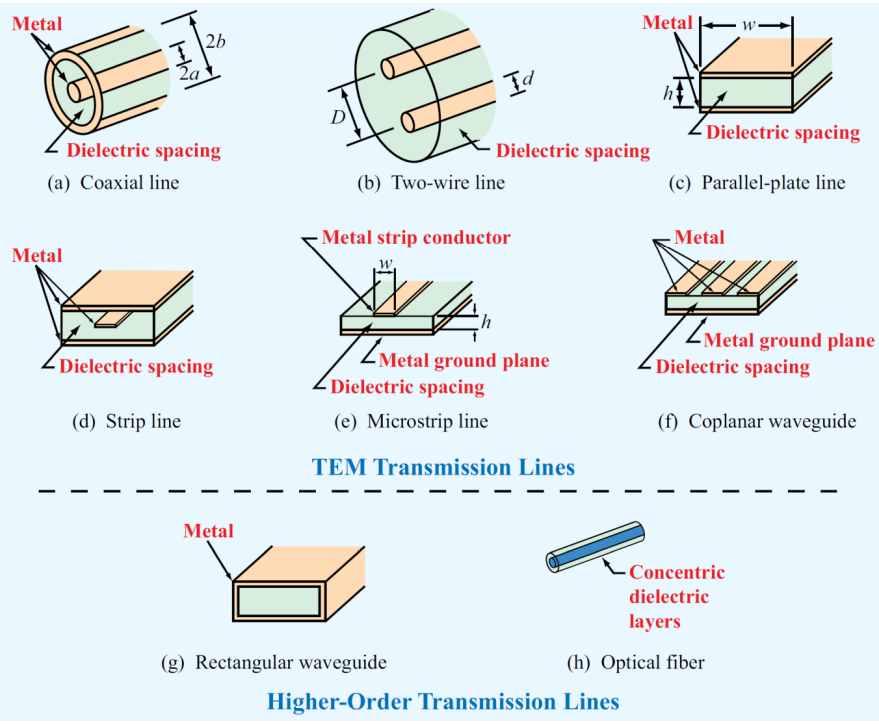
결국 다 동축으로 생각하면 됩니다.

conformal mapping

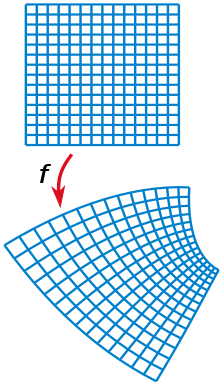
등각변환을 이용한 매핑을 통해
전부 동축과 같은 형태로 만들 수 있습니다.
자세한 내용은 공학수학(공업수학) Dirichlet problem을 참고하면 좋을 것 같습니다.
 

Transmission Line Model

이전 전자장1에서 동축 케이블의 저항, 인덕턴스, 컨덕턴스, 커패시턴스 성분에 대해 알아보았습니다.
$R^{\prime }=\frac{R_s}{2\pi }(\frac{1}{a}+\frac{1}{b})$
$L^{\prime }=\frac{\mu }{2pi}ln(\frac{b}{a})$
$G^{\prime }=$
$C^{\prime }=$

동축케이블에서 전압 전류 관계를 알기위해 
동축케이블을 미소길이$\mathrm{\Delta }z$ 로 쪼갠다고 상상해봅시다.

토막 각각은 저항, 인덕턴스, 컨덕턴스, 커패시턴스 성분을 가지고 있을 것입니다.
다음 그림과 같이 말이죠.

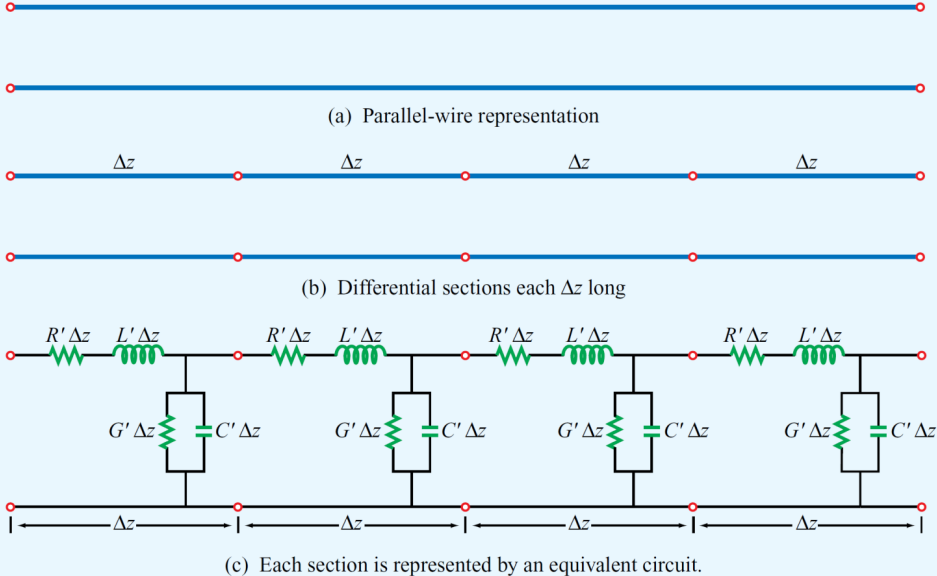
여기에 KVL(Kirchhoff's voltage law)과 KCL(Kirchhoff's current law)를 적용해봅시다.

KVL

$v(z,t)$ 부터 $v(z+\mathrm{\Delta }z,t)$ 까지 루프에 적용해보겠습니다.
$v(z,t)-R^{\prime }\mathrm{\Delta }zi(z,t)-L^{\prime }\mathrm{\Delta }z\frac{di(z,t)}{dt}-v(z+dz,t)=0$
$-\frac{v(z+\mathrm{\Delta }z,t)-v(z,t)}{\mathrm{\Delta }z}=R^{\prime }i(z,t)+L^{\prime }\frac{\partial i(z,t)}{\partial t}$
결론
$-\frac{\partial v(z,t)}{\partial z}=R^{\prime }i(z,t)+L^{\prime }\frac{\partial i(z,t)}{\partial t}$
 

KCL 

N+1 노드에 KCL을 적용해보겠습니다.
$R=\frac{1}{G^{\prime }\mathrm{\Delta }z}$ $I=C\frac{dv}{dt}$ 를 이용하면
결론
$-\frac{\partial i(z,t)}{\partial z}=G^{\prime }v(z,t)+C\frac{\partial v(z,t)}{\partial t}$
 
KCL과 KVL을 통해 두 식이 도출되었습니다. 
$ -\frac{\partial v(z,t)}{\partial z}=R' i(z,t)+L'\frac{\partial i(z,t)}{\partial t}$
$ -\frac{\partial i(z,t)}{\partial z}=G' v(z,t)+C\frac{\partial v(z,t)}{\partial t} $

두 식을 페이저 변환을 하게되면
익숙한 식이 나옵니다.
$-\frac{d\tilde{V}(z)}{dz}=(R^{\prime }+j\omega L^{\prime })\tilde{I}(z)$
$-\frac{d\tilde{I}(z)}{dz}=(G^{\prime }+j\omega C^{\prime })\tilde{V}(z)$
 
이 식은 앞서 전기장과 자기장을 배울 때 나온 식과 아주 유사합니다.
 
7장 전기장, 자기장과 비슷하게 해석하면
$\frac{d^2\text{widetilda}V(z)}{d{z}^2}-{\gamma }^2\tilde{V}(z)=0$ 
$\frac{d^{2}\widetilda{I}(z)}{dz^{2}} -\gamma^{2}\widetilde{I}(z)=0$ 
이때 감마 제곱 ${\gamma }^2$은 $(R^{\prime }+j\omega L^{\prime })(G^{\prime }+j\omega C^{\prime })$ 입니다.
 
마찬가지로 일반해는 다음과 같이 얻을 수 있습니다.
$\tilde{V}(z)=V_0^{+}{e}^{-rz}+V_0^{-}{e}^{+rz}$
$\widetilde{I}(z)=I_{0}^{+} e^{-rz}+ I_{0}^{-} e^{+rz} $

여기서 $V_0^{+},V_0^{-}$는 복소수이며 또한
아시다시피 $e^{-rz}$ 는 오른쪽으로 진행
 $e^{+rz}$ 는 왼쪽으로 진행하는 신호입니다.

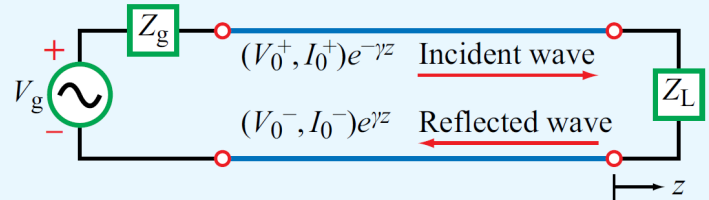
이는 앞의 8장 입사, 반사파에서 배운 진행파에 대응됩니다. 
 
 

Characteristic impedance $Z_0$

여기서도 마찬가지로 impedance를 정의하는데요.

전기장과 자기장의 비가 intrinsic impedance $\eta$였다면 ($\eta =\frac{E_0^{+}}{H_0^{+}}$)
전압과 전류의 비는 Characteristic impedance $Z_0$ 라고 합니다.
$Z_0=\frac{V_0^{+}}{I_0^{+}}$

전기장 E 대신 전압 V, 자기장 H 대신 전류 I가 대체된 것 같아 보이는데요.

Z는 다음과 같이 나옵니다.
using $-\frac{d\tilde{V}(z)}{dz}=(R^{\prime }+j\omega L^{\prime })\tilde{I}(z)$
-> $\tilde{I}(z)=-\frac{\gamma }{(R^{\prime }+j\omega L^{\prime })}(V_0^{+}{e}^{-\gamma z}-V_0^{-}{e}^{\gamma z})$
$Z_0=\frac{(R^{\prime }+j\omega L^{\prime })}{\gamma }=\sqrt{\frac{R^{\prime }+j\omega L^{\prime }}{G^{\prime }+j\omega C^{\prime }}}$

Lossless 전송선

저항과 컨덕턴스를 0으로 둔 상황에 대해 알아보겠습니다. 
즉  $R^{\prime }<<\omega L\mathrm{\$},$G'<< \omega C'$인 상황입니다. - R' G' 제거
$\gamma$는 복소수이므로 다음과 같이 나타낼 수 있습니다. 
$\gamma =\alpha +j\beta =j\omega \sqrt{L^{\prime }{C}^{\prime }}$
이때 $\beta$는 파수 k와 같고
$\alpha$는 0입니다.

이 식을 이용하면 전송선에서는 파가 빛의 속도로 전파됨을 알 수 있습니다?
동축에서 $\beta =\omega \sqrt{\mu \epsilon }$
$u_p=\frac{1}{\sqrt{\mu \epsilon }}$
이므로 빛의 속도
$c=\frac{1}{\sqrt{\mu \epsilon }}$ 와 같음을 알 수 있습니다.

 

전압 반사 계수 Voltage Reflection Coefficient

 
아까 일반해를 구할 때 입사 반사파와 식의 형태가 같다고 언급했습니다.
이와 연결시켜 해석해봅시다.
 
전원과 부하가 있는 lossless 전송선을 생각해봅시다.
해로 도출된 전압과 전류 식에서 이를 입사, 반사 성분으로 볼 수 있고
식으로 나타내보겠습니다.
$\tilde{V}(z)=V_0^{+}{e}^{-j\beta z}+V_0^{-}{e}^{j\beta z}$
$\widetilde{I}(z)=\frac{V_{0}^{+}}{Z_{0}}e^{-j\beta z}- \frac{V_{0}^{-}}{Z_{0}}e^{j\beta z} $
부하 $Z_L$ 이 있을 때는 부하를 투과 성분이라 할 수 있는데요.
 
이전 전기장, 자기장에서 표현할 때와 마찬가지로 이해하기 쉽게 A B C로 표현해보겠습니다.
전압에서 A+B=C
전류에서 A/Z - B/Z = C/ZL
반사계수는 ~~~$\mathrm{\Gamma }==\frac{Z_L-Z_0}{Z_L+Z_0}$ 로 나옵니다.
 
이때 $z_L$ 을 새로 정의합니다. 
(normalized load impedance)
$z_L=\frac{Z_L}{Z_0}$
즉
$$\mathrm{\Gamma }=\frac{z_L-1}{z_L+1}$$
과 같습니다.
($$=\frac{\frac{Z_L}{Z_0}-1}{\frac{Z_L}{Z_0}+1}$$)
반대로 load impedance $z_L$을 반사계수 $\mathrm{\Gamma }$로 나타내면
$z_L=\frac{1+\mathrm{\Gamma }}{1-\mathrm{\Gamma }}$
 

실제로 RL 회로에서 반사 성분이 크다면 신호가 왜곡될 것입니다.
일반적으로 0과 1 신호를 보내지만 반사 성분이 존재한다면 신호가 많이 틀어지겠죠.
때문에 설계 시 반사계수를 0에 가깝게 만드는 것이 중요합니다.
이를 매칭이라 합니다.